
分析 原不等式即为m≥$\frac{\sqrt{x}+\sqrt{y}}{\sqrt{x+y}}$,令z=$\frac{\sqrt{x}+\sqrt{y}}{\sqrt{x+y}}$,两边平方,再由基本不等式可得z的最大值,即可得到m的最小值.
解答 解:不等式$\sqrt{x}+\sqrt{y}≤m\sqrt{x+y}$,即为
m≥$\frac{\sqrt{x}+\sqrt{y}}{\sqrt{x+y}}$,
令z=$\frac{\sqrt{x}+\sqrt{y}}{\sqrt{x+y}}$,则z2=$\frac{x+y+2\sqrt{xy}}{x+y}$≤$\frac{x+y+(x+y)}{x+y}$=2,
即有z≤$\sqrt{2}$,(当且仅当x=y取得最大值),
即有m≥$\sqrt{2}$.即m的最小值为$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查不等式的恒成立问题的解法,考查最值的求法,注意运用基本不等式,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}{π^2}}}{4}-1$ | B. | $\frac{{3{π^2}}}{4}-1$ | C. | $\frac{{3{π^2}}}{2}-1$ | D. | $\frac{π^2}{2}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
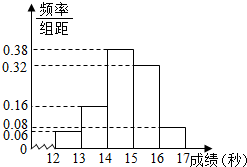 某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.
某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com