
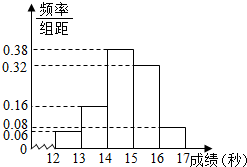
 ijѧУ�����꼶800��ѧ����һ�ΰ��ײ����У��ɼ�ȫ����12�뵽17��֮�䣬��ȡ����50�������������Խ�������·�ʽ�ֳ����飺��һ��[12��13�����ڶ���[13��14��������������[16��17]����ͼ�Ǹ�����������õ���Ƶ�ʷֲ�ֱ��ͼ��
ijѧУ�����꼶800��ѧ����һ�ΰ��ײ����У��ɼ�ȫ����12�뵽17��֮�䣬��ȡ����50�������������Խ�������·�ʽ�ֳ����飺��һ��[12��13�����ڶ���[13��14��������������[16��17]����ͼ�Ǹ�����������õ���Ƶ�ʷֲ�ֱ��ͼ������ ����1����Ƶ�ʷֲ�ֱ��ͼ���óɼ�С��13���Ƶ��Ϊ0.06���ɴ����������������ΰ��ײ����гɼ������������
��2����Ƶ�ʷֲ�ֱ��ͼ���õ�����[14��15����Ƶ��Ϊ0.38���ɴ��ܹ��Ʊ��꼶800��ѧ���У��ɼ����ڵ������������
��2����Ƶ�ʷֲ�ֱ��ͼ�����������õ���һ������1��Ů��2������������������3��Ů��1���������ɴ˵æεĿ���ȡֵΪ1��2��3���ֱ������Ӧ�ĸ��ʣ��Ӷ�������εķֲ��к�������
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ���óɼ�С��13���Ƶ��Ϊ0.06��
�����������ΰ��ײ����гɼ����������Ϊ��
0.06��50=3���ˣ���
��2����Ƶ�ʷֲ�ֱ��ͼ���õ�����[14��15����Ƶ��Ϊ0.38��
����Ʊ��꼶800��ѧ���У��ɼ����ڵ����������Ϊ��
800��0.38=304���ˣ���
��2����Ƶ�ʷֲ�ֱ��ͼ���õ�һ���Ƶ��Ϊ0.06���������Ƶ��Ϊ0.08��
���һ����50��0.06=3�ˣ���������50��0.08=4�ˣ�
�������е�һ��ֻ��һ��Ů����������ֻ��һ��������
���һ������1��Ů��2������������������3��Ů��1��������
�ִӵ�һ���������и���ȡ2��ѧ�����һ��ʵ���飬��������������Ϊ�Σ�
��εĿ���ȡֵΪ1��2��3��
P����=1��=$\frac{{C}_{2}^{1}{C}_{1}^{1}}{{C}_{3}^{2}}•\frac{{C}_{3}^{2}}{{C}_{4}^{2}}$=$\frac{1}{3}$��
P����=2��=$\frac{{C}_{2}^{2}}{{C}_{3}^{2}}•\frac{{C}_{3}^{2}}{{C}_{4}^{2}}+\frac{{C}_{2}^{1}{C}_{1}^{1}}{{C}_{3}^{2}}•\frac{{C}_{3}^{1}{C}_{1}^{1}}{{C}_{4}^{2}}$=$\frac{1}{2}$��
P����=3��=$\frac{{C}_{2}^{2}}{{C}_{3}^{2}}•\frac{{C}_{3}^{1}{C}_{1}^{1}}{{C}_{4}^{2}}$=$\frac{1}{6}$��
��εķֲ���Ϊ��
| �� | 1 | 2 | 3 |
| P | $\frac{1}{3}$ | $\frac{1}{2}$ | $\frac{1}{6}$ |
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬ע��Ƶ�ʷֲ�ֱ��ͼ�����ʺ͵ȿ����¼����ʼ��㹫ʽ�ĺ������ã�


 ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|1��x��2} | B�� | {x|1��x��2} | C�� | {x|x��1} | D�� | {x|1��x��2} |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com