
分析 根据函数的性质求出命题的等价条件,结合复合命题真假之间的关系进行求解即可.
解答 解:函数y=x2+mx+1在[-1,+∞)上单调递增,
则对称性满足-$\frac{m}{2}$≤-1,即m≥2,
若y=4x2+4(m-2)x+1>0恒成立,
则判别式△=16(m-2)2-16<0,
即(m-2)2<1,
即-1<m-2<1,即1<m<3,
若命题“p或q”为真,命题“p且q”为假,
则p,q为一真一假,
若p真q假,则$\left\{\begin{array}{l}{m≥2}\\{m≥3或m≤1}\end{array}\right.$,即m≥3,
若p假q真,则$\left\{\begin{array}{l}{m<2}\\{1<m<3}\end{array}\right.$,即1<m<2,
故实数m的取值范围是m≥3或1<m<2.
点评 本题主要考查复合命题的真假关系的应用,根据条件求出命题的等价条件是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
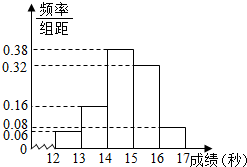 某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.
某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
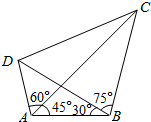 如图,在平面四边形ABCD中,AB=5$\sqrt{2}$,∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.
如图,在平面四边形ABCD中,AB=5$\sqrt{2}$,∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com