
分析 (1)直接采用零点分段法确定函数的最值;
(2)先假设存在,再两次运用基本不等式得出${a}^{\frac{5}{2}}•{b}^{\frac{5}{2}}$≤$\frac{1}{2}$和${a}^{\frac{5}{2}}•{b}^{\frac{5}{2}}$≥$\frac{2}{3}$相互矛盾,所以假设不成立.
解答 解:(1)分三类讨论如下:
①当x<-1时,f(x)=x+4,单调递增,f(x)<3;
②当-1≤x≤$\frac{1}{2}$时,f(x)=-5x-2,单调递减,f(x)max=f(-1)=3,
③当x>$\frac{1}{2}$时,f(x)=-x-4,单调递减,f(x)<f($\frac{1}{2}$)=-$\frac{9}{2}$,
综合以上讨论得,f(x)的最大值M=3;
(2)假设存在正数a,b,使得a6+b6=$\sqrt{ab}$≥2$\sqrt{a^6b^6}$=2a3b3,
所以,${a}^{\frac{5}{2}}•{b}^{\frac{5}{2}}$≤$\frac{1}{2}$,------------①
又因为$\frac{1}{a^3}$+$\frac{1}{b^3}$=Mab=3ab≥2•$\frac{1}{\sqrt{a^3b^3}}$,
所以,${a}^{\frac{5}{2}}•{b}^{\frac{5}{2}}$≥$\frac{2}{3}$,-----------②
显然①②相互矛盾,
所以,假设不成立,即不存在a,b使得a6+b6=$\sqrt{ab}$.
点评 本题主要考查了分段函数最值的确定,以及基本不等式在解题中的应用,运用了零点分段法和反证法,属于中档题.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}{π^2}}}{4}-1$ | B. | $\frac{{3{π^2}}}{4}-1$ | C. | $\frac{{3{π^2}}}{2}-1$ | D. | $\frac{π^2}{2}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
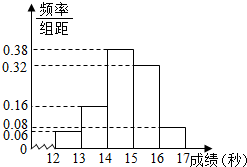 某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.
某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
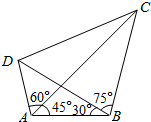 如图,在平面四边形ABCD中,AB=5$\sqrt{2}$,∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.
如图,在平面四边形ABCD中,AB=5$\sqrt{2}$,∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com