设函数f(x)=x3-ax,x∈R.过图象上一点斜率最小的切线平行于直线x+y=2.
(1)求a的值;
(2)求函数f(x)的单调区间和极值;
(3)已知当x∈(1,+∞)时,f(x)-kf(x-1)≥0恒成立,求实数k的取值范围.
【答案】
分析:(1)由f(x)=x
3-ax,x∈R,得f′(x)=3x
2-a≥-a,由过图象上一点斜率最小的切线的斜率k=-a和过图象上一点斜率最小的切线平行于直线x+y=2,能求出a.
(2)由(1)知f(x)=x
3-x,f′(x)=3x
2-1,令f′(x)=3x
2-1=0,得x=
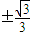
.列表讨论能求出函数f(x)的单调区间和极值.
(3)由f(x)-kf(x-1)≥0,f(x)=x
3-x,得k≤
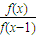
=
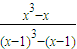
=1+
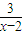
,由此能求出k有范围.
解答:解:(1)∵f(x)=x
3-ax,x∈R,
∴f′(x)=3x
2-a≥-a,
∴过图象上一点斜率最小的切线的斜率k=-a,
∵过图象上一点斜率最小的切线平行于直线x+y=2,
∴-a=-1,故a=1.
(2)∵a=1,∴f(x)=x
3-x,f′(x)=3x
2-1,
令f′(x)=3x
2-1=0,得x=
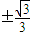
.
列表讨论:
| x | (-∞,-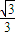 ) ) | - | (-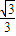 , ,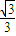 ) ) | 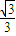 | (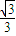 ,+∞) ,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | ↑ | 极大值 | ↓ | 极小值 | ↑ |
由表讨论知:函数f(x)的单调增区间是 (-∞,-
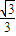
)、(
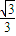
,+∞);单调减区间是(-
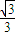
,
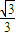
).
极大值f(-
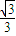
)=-
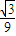
+
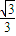
=
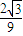
,
极小值f(
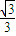
)=
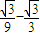
=-
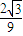
.
(3)∵f(x)-kf(x-1)≥0,f(x)=x
3-x,
∴k≤
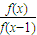
=
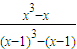
=
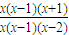
=
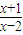
=1+
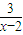
,
∵x∈(1,+∞),
当1<x<2时,-2<1+
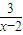
<1
当x=-2时,1+
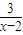
<+∞,
当x>2时,1+
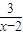
>1
∴k≤-2.
点评:本题考查实数值的求法,考查单调区间和极值的求法,考查实数的取值范围的求法.解题时要认真审题,仔细解答,注意列表讨论法和分离变量法的灵活运用.

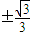 .列表讨论能求出函数f(x)的单调区间和极值.
.列表讨论能求出函数f(x)的单调区间和极值.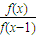 =
=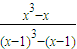 =1+
=1+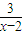 ,由此能求出k有范围.
,由此能求出k有范围.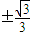 .
.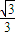 )
)
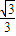 ,
,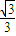 )
)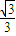
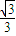 ,+∞)
,+∞)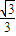 )、(
)、(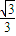 ,+∞);单调减区间是(-
,+∞);单调减区间是(-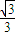 ,
,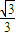 ).
).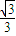 )=-
)=-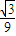 +
+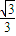 =
=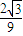 ,
,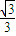 )=
)=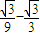 =-
=-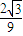 .
.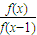 =
=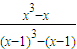
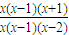
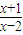
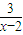 ,
,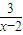 <1
<1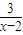 <+∞,
<+∞,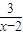 >1
>1
