
 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
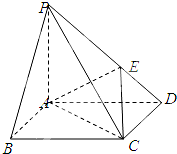 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=1,点E在PD上,且PE:ED=2:1.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=1,点E在PD上,且PE:ED=2:1.查看答案和解析>>
科目:高中数学 来源: 题型:
| AP |
| AB |
| CP |
| 3 |
| 4 |
| CA |
| 1 |
| 4 |
| CB |
| CP |
| AB |
| AP |
| PB |
查看答案和解析>>
科目:高中数学 来源: 题型:
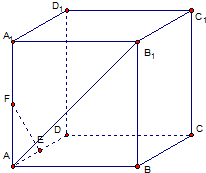 如图,在正方体ABCD-A1B1C1D1中,E、F分别是AD,AA1的中点
如图,在正方体ABCD-A1B1C1D1中,E、F分别是AD,AA1的中点查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 4 |
| y2 |
| 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:
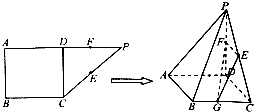 如图,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=
如图,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=| 1 |
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
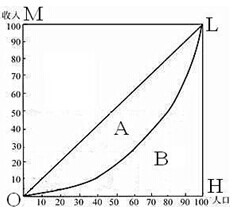 基尼系数是衡量一个国家贫富差距的标准.图中横轴OH表示人口(按收入由低到高分组)的累积百分比,纵轴OM表示收入的累积百分比,弧线OL(洛伦兹曲线)与对角线之间的面积A叫做“不平等面积”,折线段OHL与对角线之间的面积(A+B)叫做“完全不平等面积”,不平等面积与完全不平等面积之比等于基尼系数,则:
基尼系数是衡量一个国家贫富差距的标准.图中横轴OH表示人口(按收入由低到高分组)的累积百分比,纵轴OM表示收入的累积百分比,弧线OL(洛伦兹曲线)与对角线之间的面积A叫做“不平等面积”,折线段OHL与对角线之间的面积(A+B)叫做“完全不平等面积”,不平等面积与完全不平等面积之比等于基尼系数,则:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com