
| A. | 1,$2,-\frac{π}{6}$ | B. | 2,$2,-\frac{π}{3}$ | C. | 1,$4,-\frac{π}{6}$ | D. | 2,$4,\frac{π}{3}$ |
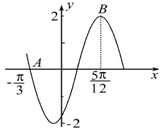
分析 由图象的最值可求得A,由$\frac{3}{4}$T=$\frac{5π}{12}$-(-$\frac{π}{3}$)=$\frac{3π}{4}$,可求得ω,最后利用五点作图法”求得φ即可得到答案.
解答 解:由图知,A=2,$\frac{3}{4}$T=$\frac{5π}{12}$-(-$\frac{π}{3}$)=$\frac{3π}{4}$,
故T=$\frac{2π}{ω}$=π,解得:ω=2.
由“五点作图法”知:2×$\frac{5π}{12}$+φ=$\frac{π}{2}$,故φ=-$\frac{π}{3}$,
所以,A,ω,φ的值分别是:2,2,-$\frac{π}{3}$.
故选:B.
点评 本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,利用“五点作图法”求得φ是难点,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
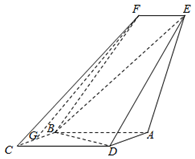 如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=$\sqrt{6}$,DE=3,∠BAD=60°,G为BC的中点.
如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=$\sqrt{6}$,DE=3,∠BAD=60°,G为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
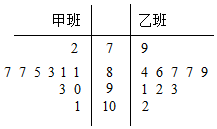 某学校为了分析在一次数学竞赛中甲、乙两个班的数学成绩,分别从甲、乙两个班中随机抽取了10个学生的成绩,成绩的茎叶图如下:
某学校为了分析在一次数学竞赛中甲、乙两个班的数学成绩,分别从甲、乙两个班中随机抽取了10个学生的成绩,成绩的茎叶图如下:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com