
【题目】设函数f(x)=loga(1﹣![]() ),其中0<a<1.
),其中0<a<1.
(Ⅰ)证明:f(x)是(a,+∞)上的减函数;
(Ⅱ)若f(x)>1,求x的取值范围.
【答案】解:(Ⅰ)设0<a<x1<x2 , g(x)=1﹣![]() ,
,
则g(x1 )﹣g(x2)=(1﹣![]() )﹣(1﹣
)﹣(1﹣![]() )=
)=![]() <0,
<0,
∴g(x1 )<g(x2 ),
又∵0<a<1,
∴f(x1 )>f(x2 ),
∴f(x)在(a,+∞)递减;
(Ⅱ)∵![]() >1,
>1,
∴0<1﹣![]() <a,
<a,
∴1﹣a<![]() <1,
<1,
∵0<a<1,
∴1﹣a>0,
从而a<x<![]() ,
,
∴x的范围是(a,![]() ).
).
【解析】(Ⅰ)设0<a<x1<x2 , g(x)=1﹣![]() , 则g(x1 )﹣g(x2)=
, 则g(x1 )﹣g(x2)=![]() <0,进而f(x1 )>f(x2 ),得f(x)在(a,+∞)递减;
<0,进而f(x1 )>f(x2 ),得f(x)在(a,+∞)递减;
(Ⅱ)由![]() >1,得1﹣a<<1,从而a<x<
>1,得1﹣a<<1,从而a<x<![]() , 从而求出x的范围.
, 从而求出x的范围.
【考点精析】通过灵活运用利用导数研究函数的单调性,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减即可以解答此题.
在这个区间单调递减即可以解答此题.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】5个球放入3个盒子,在下列不同条件下,各有多少种投放方法?
①小球不同,盒子不同,盒子不空
②小球不同,盒子不同,盒子可空
③球不同,盒子相同,盒子不空
④小球不同,盒子相同,盒子可空
⑤小球相同,盒子不同,盒子不空
⑥小球相同,盒子不同,盒子可空
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某销售公司为了解员工的月工资水平,从1000位员工中随机抽取100位员工进行调查,得到如下的频率分布直方图:
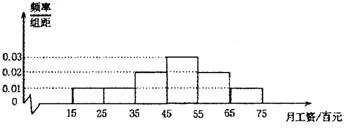
(1)试由此图估计该公司员工的月平均工资;
(2)该公司工资发放是以员工的营销水平为重要依据来确定的,一般认为,工资低于4500。元的员工属于学徒阶段,没有营销经验,若进行营销将会失败;高于4500元的员工是具备营销成熟员工,基进行营销将会成功。现将该样本按照“学徒阶段工资”、“成熟员工工资”分成两层,进行分层抽样,从中抽出5人,在这5人中任选2人进行营销活动。活动中,每位员工若营销成功,将为公司赢得3万元,否则公司将损失1万元。试问在此次比赛中公司收入多少万元的可能性最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经国务院批复同意,郑州成功入围国家中心城市,某校学生团针对“郑州的发展环境”对20名学生进行问卷调查打分(满分100分),得到如图1所示茎叶图.
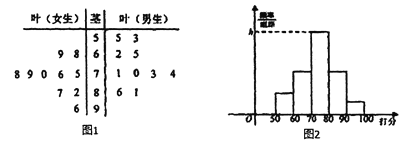
(1)分别计算男生女生打分的平均分,并用数学特征评价男女生打分的数据分布情况;
(2)如图2按照打分区间![]() 绘制的直方图中,求最高矩形的高;
绘制的直方图中,求最高矩形的高;
(3)从打分在70分以下(不含70分)的同学中抽取3人,求有女生被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据某市地产数据研究的数据显示,2016年该市新建住宅销售均价走势如下图所示,为抑制房价过快上涨,政府从8月份开始采取宏观调控措施,10月份开始房价得到很好的抑制.
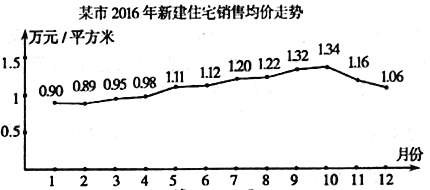
(1)地产数据研究院发现,3月至7月的各月均价![]() (万元/平方米)与月份
(万元/平方米)与月份![]() 之间具有较强的线性相关关系,试建立
之间具有较强的线性相关关系,试建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);政府若不调控,依此相关关系预测第12月份该市新建住宅销售均价;
的回归方程(系数精确到0.01);政府若不调控,依此相关关系预测第12月份该市新建住宅销售均价;
(2)地产数据研究院在2016年的12个月份中,随机抽取三个月的数据作样本分析,若关注所抽三个月的所属季度,记不同季度的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据及公式: ![]() ,
, ![]() ,
, ![]() ;
;
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,若Ω是长方体ABCD﹣A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1 , 则下列结论中不正确的是( )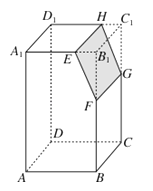
A.EH∥FG
B.四边形EFGH是矩形
C.Ω是棱柱
D.Ω是棱台
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB,E,F,G,H分别为PC、PD、BC、PA的中点.
求证:(1)PA∥平面EFG;
(2)DH⊥平面EFG.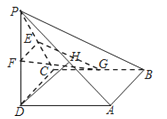
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医学院欲研究昼夜温差大小与患感冒人数多少之间的关系,该协会分别到气象局与某医院抄录了1到6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到数据资料见下表:

该院确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(Ⅰ)求选取的2组数据恰好是不相邻的两个月的概率;
(Ⅱ)已知选取的是1月与6月的两组数据.
(1)请根据2到5月份的数据,求出就诊人数![]() 关于昼夜温差
关于昼夜温差![]() 的线性回归方程;
的线性回归方程;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该协会所得线性回归方程是否理想?
(参考公式和数据: 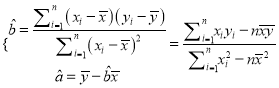
![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com