
【题目】(本小题满分为14分)已知定义域为R的函数![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
【答案】(1)a=2,b=1.(2)![]()
【解析】
试题分析:(1)利用奇函数性质列出两个独立条件解出a,b的值,注意要验证. 因为定义域为R,所以有f(0)=0,从而b=1.再取f(1)=-f(-1)得a=2,代入函数验证![]() (2)利用函数奇偶性及单调性化简不等式:因f(x)是奇函数,从而不等式f(t2-2t)+f(2t2-k)<0等价于f(t2-2t)<-f(2t2-k)=f(-2t2+k). 因为f(x)是减函数,其又等价于t2-2t>-2t2+k.对一切t∈R恒成立,即Δ=4+12k<0,解得
(2)利用函数奇偶性及单调性化简不等式:因f(x)是奇函数,从而不等式f(t2-2t)+f(2t2-k)<0等价于f(t2-2t)<-f(2t2-k)=f(-2t2+k). 因为f(x)是减函数,其又等价于t2-2t>-2t2+k.对一切t∈R恒成立,即Δ=4+12k<0,解得![]()
试题解析: (1)因为f(x)是奇函数,且定义域为R,所以f(0)=0,
即![]() =0,解得b=1.
=0,解得b=1.
从而有![]() .又由f(1)=-f(-1)知
.又由f(1)=-f(-1)知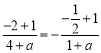 ,解得a=2----6分
,解得a=2----6分
经检验适合题意,∴a=2,b=1.
(2)由(1)知![]()
由上式易知f(x)在(-∞,+∞)上为减函数.又因f(x)是奇函数,
从而不等式f(t2-2t)+f(2t2-k)<0等价于f(t2-2t)<-f(2t2-k)=f(-2t2+k).-----10分
因为f(x)是减函数,由上式推得t2-2t>-2t2+k.
即对一切t∈R有3t2-2t-k>0.
从而判别式Δ=4+12k<0,解得![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn= ![]() +
+ ![]() .
.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=an+2﹣an+ ![]() ,且数列{bn}的前n项和为Tn , 求证:Tn<2n+
,且数列{bn}的前n项和为Tn , 求证:Tn<2n+ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学准备参加学校在寒假里组织的“社区服务”、“进敬老院”、“参观工厂”、“民俗调查”、“环保宣传”五个项目的社会实践活动,每天只安排一项活动,并要求在周一至周五内完成.其中“参观工厂”与“环保宣讲”两项活动必须安排在相邻两天,“民俗调查”活动不能安排在周一.则不同安排方法的种数是( )
A.48 B.24 C.36 D.64
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如表频率分布表:
分组 | 频数 | 频率 |
[39.95,39.97) | 6 | P1 |
[39.97,39.99) | 12 | 0.20 |
[39.99,40.01) | a | 0.50 |
[40.01,40.03) | b | P2 |
合计 | n | 1.00 |
(1)求a、b、n及P1、P2的值,并画出频率分布直方图(结果保留两位小数); 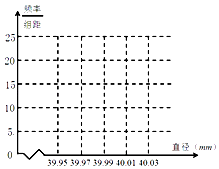
(2)已知标准乒乓球的直径为40.00mm,直径误差不超过0.01mm的为五星乒乓球,若这批乒乓球共有10000个,试估计其中五星乒乓球的数目;
(3)统计方法中,同一组数据常用该组区间的中点值(例如区间[39.99,40.01)的中点值是40.00)作为代表,估计这批乒乓球直径的平均值和中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意m∈R,直线mx﹣y+1=0与圆x2+y2=r2(r>0)交于不同的两点A、B,且存在m使| ![]() +
+ ![]() |≥|
|≥| ![]() |(O是坐标原点)成立,那么r的取值范围是( )
|(O是坐标原点)成立,那么r的取值范围是( )
A.0<r≤ ![]()
B.1<r< ![]()
C.1<r≤ ![]()
D.r> ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:y=2x+m与圆O:x2+y2=1相交于A,B两个不同的点,且A(cosα,sinα),B(cosβ,sinβ).
(1)当△AOB面积最大时,求m的取值,并求出|AB|的长度.
(2)判断sin(α+β)是否为定值;若是,求出定值的大小;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设双曲线 ![]() =1(a>0,b>0)的右焦点为F,右顶点为A,过F作AF的垂线与双曲线的两条渐近线交于B、C两点,过B、C分别作AC、AB的垂线,两垂线交于点D.若D到直线BC的距离小于2(a+
=1(a>0,b>0)的右焦点为F,右顶点为A,过F作AF的垂线与双曲线的两条渐近线交于B、C两点,过B、C分别作AC、AB的垂线,两垂线交于点D.若D到直线BC的距离小于2(a+ ![]() ),则该双曲线的离心率的取值范围是( )
),则该双曲线的离心率的取值范围是( )
A.(1,2)
B.( ![]() ,2)
,2)
C.(1, ![]() )
)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)如图,四棱锥![]() 的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,
的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,连结
的中点,连结![]() .求证:
.求证:
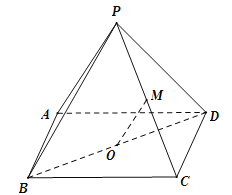
(1)![]() ∥平面
∥平面![]() ;
;
(2)![]() ⊥平面
⊥平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10000m,速度为180km(千米)/h(小时),飞机先看到山顶的俯角为15°,经过420s(秒)后又看到山顶的俯角为45°,求山顶的海拔高度(取 ![]() ,
, ![]() ).
). 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com