
| A. | [-40,40] | B. | [-30,30] | C. | [-15,15] | D. | [-10,10] |
分析 如图所示,由题意可得|$\overline{DA}$|=6,当$\overrightarrow{PQ}$的长度的最大值为5.求得$\overrightarrow{PQ}$•$\overrightarrow{DA}$的最小值和最大值,可得$\overrightarrow{PQ}$•$\overrightarrow{DA}$的取值范围.
解答  解:如图所示,由题意可得|$\overline{DA}$|=6,当$\overrightarrow{PQ}$的长度的最大值为5,
解:如图所示,由题意可得|$\overline{DA}$|=6,当$\overrightarrow{PQ}$的长度的最大值为5,
故当$\overrightarrow{PQ}$的长度的最大且$\overrightarrow{PQ}$ 与$\overrightarrow{DA}$反向时,则$\overrightarrow{PQ}$•$\overrightarrow{DA}$取得最小值为5×6×cosπ=-30,
故当$\overrightarrow{PQ}$的长度的最大且$\overrightarrow{PQ}$ 与$\overrightarrow{DA}$同向时,则$\overrightarrow{PQ}$•$\overrightarrow{DA}$取得最大值为5×6×cos0=30,
故则$\overrightarrow{PQ}$•$\overrightarrow{DA}$的取值范围为[-30,30],
故选:B.
点评 本题主要考查两个向量的数量积的定义,属于基础题.


科目:高中数学 来源: 题型:解答题
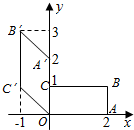 如图,矩形OABC在变换T的作用下变成了平行四边形OA′B′C′,变换T所对应的矩阵为M,矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍的变换所对应的矩阵.
如图,矩形OABC在变换T的作用下变成了平行四边形OA′B′C′,变换T所对应的矩阵为M,矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍的变换所对应的矩阵.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 统计某学校高二年级某班40名学生的数学期中考试成绩,分数均在40分至100分之间,得到的频率分布直方图如图所示,则成绩不低于60分的人数有32.
统计某学校高二年级某班40名学生的数学期中考试成绩,分数均在40分至100分之间,得到的频率分布直方图如图所示,则成绩不低于60分的人数有32.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
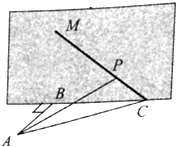 如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练,已知点A到墙面的距离为AB,某目标点P沿墙面的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若BC=10m,AC=20m,∠BCM=45°,则tanθ的最大值为$\frac{2\sqrt{3}}{3}$.(仰角θ为直线AP与平面ABC所成角)
如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练,已知点A到墙面的距离为AB,某目标点P沿墙面的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若BC=10m,AC=20m,∠BCM=45°,则tanθ的最大值为$\frac{2\sqrt{3}}{3}$.(仰角θ为直线AP与平面ABC所成角)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com