
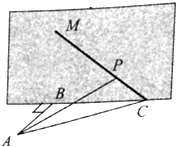
 如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练,已知点A到墙面的距离为AB,某目标点P沿墙面的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若BC=10m,AC=20m,∠BCM=45°,则tanθ的最大值为$\frac{2\sqrt{3}}{3}$.(仰角θ为直线AP与平面ABC所成角)
如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练,已知点A到墙面的距离为AB,某目标点P沿墙面的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若BC=10m,AC=20m,∠BCM=45°,则tanθ的最大值为$\frac{2\sqrt{3}}{3}$.(仰角θ为直线AP与平面ABC所成角) 分析 如图由点P向BC作垂线,连结AG,则∠PAG=θ,求得∠ACB,表示出tanθ的表达式,利用二次函数的性质确定最大值.
解答  解:如图由点P向BC作垂线,连结AG,则∠PAG=θ,
解:如图由点P向BC作垂线,连结AG,则∠PAG=θ,
∵BC=10,AC=20,
∴∠ACB=60°,
AG=$\sqrt{C{G}^{2}+A{C}^{2}-2AC•CG•cos∠ACB}$=$\sqrt{C{G}^{2}+400-20•AG}$,
tanθ=$\frac{PG}{AG}$=$\frac{CG}{AG}$=$\sqrt{\frac{C{G}^{2}}{C{G}^{2}+400-20•CG}}$=$\sqrt{\frac{1}{\frac{400}{C{G}^{2}}-\frac{20}{CG}+1}}$,
∴当$\frac{1}{CG}$=$\frac{20}{2×400}$,即CG=40时,tanθ取最大值,
此时tanθ=$\frac{1600}{400+1600-800}$=$\frac{2\sqrt{3}}{3}$.
即tanθ的最大值为$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题主要考查解三角形问题的实际应用.解题的关键步骤是利用余弦定理表示出tanθ的表达式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-40,40] | B. | [-30,30] | C. | [-15,15] | D. | [-10,10] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100],则图中a的值为0.005.
某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100],则图中a的值为0.005.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 都大于2 | B. | 至少有一个不大于2 | ||
| C. | 都小于2 | D. | 至少有一个不小于2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 拥有手机 | 没有手机 | 合计 | |
| 成绩优秀 | |||
| 成绩不优势 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 080 | B. | 263 | C. | 140 | D. | 280 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com