
分析 (1)由条件利用正弦函数、余弦函数的奇偶性求得 cosθ=0,可得θ=$\frac{π}{2}$.再根据f($\frac{π}{4}$)=0求得a的中.
(2)由条件利用两角和的正弦公式求得f(x)的解析式,再利用正弦函数的定义域和值域求得g(x)的最值并求出相应的x的值.
解答 解:(1)∵函数f(x)=(a+2cos2x)cos(2x+θ)为奇函数为奇函数,
∴f-x)=-f(x),
即 (a+2cos2x)cos(-2x+θ)=-(a+2cos2x)cos(2x+θ),
∴cos(-2x+θ)=-cos(2x+θ),∴cos2xcosθ=0,求得 cosθ=0.
再结合θ∈(0,π),可得θ=$\frac{π}{2}$,∴f(x)=-(a+2cos2x)sin2x.
又f($\frac{π}{4}$)=-(a+2cos2$\frac{π}{4}$)sin$\frac{π}{2}$=0,∴a=-1.
(2)由 (1)有 f(x)=-(-1+2cos2x)sin2x=-cos2xsin2x=-$\frac{1}{2}$sin4x,
∴g(x)=f(x)+f(x+$\frac{π}{3}$)=-$\frac{1}{2}$sin4x-$\frac{1}{2}$sin4(x+$\frac{π}{3}$)=-$\frac{1}{2}$sin4x+$\frac{1}{2}$sin(4x+$\frac{π}{3}$)
=-$\frac{1}{2}$sin4x=-$\frac{1}{2}$sin4x+$\frac{1}{2}$sin4xcos$\frac{π}{3}$+$\frac{1}{2}$cos4xsin$\frac{π}{3}$=-$\frac{1}{4}$sin4x+$\frac{\sqrt{3}}{4}$cos4x=-$\frac{1}{2}$sin(4x-$\frac{π}{3}$).
再根据x∈[0,$\frac{π}{4}$],可得-$\frac{π}{3}$≤4x-$\frac{π}{3}$≤$\frac{2π}{3}$,
故当4x-$\frac{π}{3}$=$\frac{π}{2}$时,g(x)取得最小值为-$\frac{1}{2}$,此时,x=$\frac{5π}{24}$;
当4x-$\frac{π}{3}$=-$\frac{π}{3}$时,g(x)取得最大值为$\frac{\sqrt{3}}{4}$,此时,x=0.
点评 本题主要考查正弦函数、余弦函数的奇偶性,两角和的正弦公式,正弦函数的定义域和值域,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
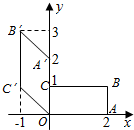 如图,矩形OABC在变换T的作用下变成了平行四边形OA′B′C′,变换T所对应的矩阵为M,矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍的变换所对应的矩阵.
如图,矩形OABC在变换T的作用下变成了平行四边形OA′B′C′,变换T所对应的矩阵为M,矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍的变换所对应的矩阵.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{2}$,$\frac{3π}{4}$)∪(π,$\frac{5π}{4}$) | B. | ($\frac{π}{4}$,$\frac{π}{2}$)∪(π,$\frac{5π}{4}$) | C. | ($\frac{π}{2}$,$\frac{3π}{4}$)∪($\frac{5π}{4}$,$\frac{3π}{2}$) | D. | ($\frac{π}{4}$,$\frac{π}{2}$)∪($\frac{3π}{4}$,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1008>b1008 | B. | a1008=b1008 | C. | a1008≥b1008 | D. | a1008≤b1008 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
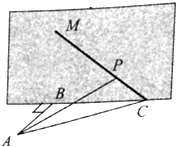 如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练,已知点A到墙面的距离为AB,某目标点P沿墙面的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若BC=10m,AC=20m,∠BCM=45°,则tanθ的最大值为$\frac{2\sqrt{3}}{3}$.(仰角θ为直线AP与平面ABC所成角)
如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练,已知点A到墙面的距离为AB,某目标点P沿墙面的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若BC=10m,AC=20m,∠BCM=45°,则tanθ的最大值为$\frac{2\sqrt{3}}{3}$.(仰角θ为直线AP与平面ABC所成角)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com