
分析 (1)根据题意设所求方程为3x+4y+a=0,根据直线与圆相切时,圆心到直线的距离d=r求出a的值,即可确定出所求直线方程;
(2)当直线与AB平行,且与圆相切时,△PAB面积的最大值,如图所示,求出|AB|与|MN|的长,即可确定出△PAB面积的最大值.
解答 解:(1)设所求直线方程为3x+4y+a=0,
由题意得:圆心(0,0)到直线的距离d=r,即$\frac{|a|}{5}$=2,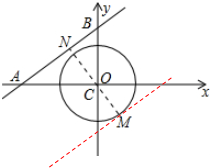
解得:a=±10,
则所求直线方程为3x+4y±10=0;
(2)当直线与AB平行,且与圆相切时,△PAB面积的最大值,
此时直线方程为3x+4y-10=0,
∵点C到直线AB的距离|CN|=$\frac{12}{5}$,CM=2,
∴|MN|=$\frac{12}{5}$+2=$\frac{22}{5}$,
∵A(-4,0),B(0,3),即OA=4,OB=3,
∴|AB|=5,
则△PAB面积最大值为$\frac{1}{2}$×5×$\frac{22}{5}$=11.
点评 此题考查了直线与圆的方程的应用,涉及的知识有:点到直线的距离公式,两直线平行时斜率的关系,以及直线与圆相切的性质,熟练掌握公式及性质是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | [-40,40] | B. | [-30,30] | C. | [-15,15] | D. | [-10,10] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 都大于2 | B. | 至少有一个不大于2 | ||
| C. | 都小于2 | D. | 至少有一个不小于2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 拥有手机 | 没有手机 | 合计 | |
| 成绩优秀 | |||
| 成绩不优势 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
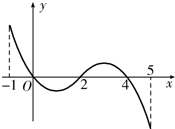 已知函数f(x)的定义域为[-1,5],部分对应值如表,
已知函数f(x)的定义域为[-1,5],部分对应值如表,| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 2 | 0 | 2 | 1 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com