
分析 (Ⅰ)由条件可得$\frac{2}{b}$=$\frac{1}{a}$+$\frac{1}{c}$>2$\sqrt{\frac{1}{ac}}$,可得$\frac{b}{a}$<$\frac{c}{b}$.
(2)由条件得到b2<ac,利用基本不等式变形,可得出cosB的范围,利用余弦函数的图象与性质,以及特殊角的三角函数值,根据B为三角形的内角,即可求出B的范围.
解答 (Ⅰ)解:∵△ABC的三边长为a、b、c,且其中任意两边长均不相等,$\frac{1}{a}$,$\frac{1}{b}$,$\frac{1}{c}$成等差数列,
∴$\frac{2}{b}$=$\frac{1}{a}$+$\frac{1}{c}$>2$\sqrt{\frac{1}{ac}}$.
∴b2<ac,
∴$\frac{b}{a}$<$\frac{c}{b}$.
(Ⅱ)证明:∵b2<ac,
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$>$\frac{1}{2}$,
∴B∈[0,$\frac{π}{3}$],
∴B不可能是钝角.
点评 此题考查了余弦定理,等差、等比数列的性质,以及基本不等式的运用,熟练掌握定理及性质是解本题的关键,属于中档题.


科目:高中数学 来源: 题型:解答题
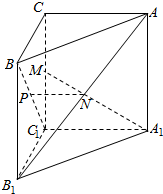 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=$\sqrt{6}$,点P、M、N分别为BC1、CC1、AB1的中点.
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=$\sqrt{6}$,点P、M、N分别为BC1、CC1、AB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b | B. | a=b | ||
| C. | a>b | D. | a,b的大小与n的取值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-40,40] | B. | [-30,30] | C. | [-15,15] | D. | [-10,10] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100],则图中a的值为0.005.
某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100],则图中a的值为0.005.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 拥有手机 | 没有手机 | 合计 | |
| 成绩优秀 | |||
| 成绩不优势 | |||
| 合计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com