
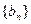 满足:
满足: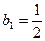 ,
,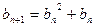 ,
, 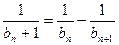 ;
;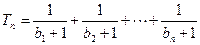 ,对任意的正整数
,对任意的正整数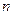 ,
,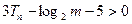 恒成立.求m的取值范围.
恒成立.求m的取值范围. 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源:不详 题型:单选题
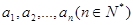 满足条件:
满足条件: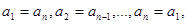
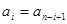 ,
,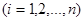 我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列
我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列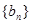 是项数不超过
是项数不超过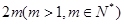 的“对称数列”,并使得
的“对称数列”,并使得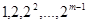 依次为该数列中连续的前
依次为该数列中连续的前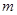 项,则数列
项,则数列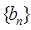 的前2009项和
的前2009项和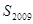 所有可能的取值的序号为 ( )
所有可能的取值的序号为 ( )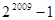 ②
②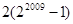 ③
③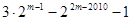 ④
④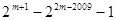
| A.①②③ | B.②③④ | C.①②④ | D.①③④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
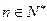 ,总有
,总有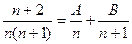 成立,求常数
成立,求常数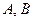 的值;
的值;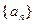 中,
中, ,
,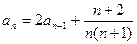 (
(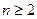 ,
,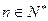 ),求通项
),求通项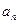 ;
;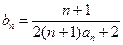 ,从数列
,从数列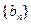 中依次取出第
中依次取出第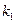 项,第
项,第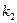 项,…第
项,…第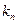 项,按原来的顺序组成新
项,按原来的顺序组成新 的数列
的数列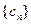 ,其中
,其中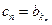 ,其中
,其中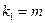 ,
,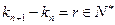 .试问是否存在正整数
.试问是否存在正整数 使
使 且
且 成立?若存
成立?若存 在,求正整数
在,求正整数 的值;不存在,说明理由.
的值;不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的前n项和记为
的前n项和记为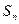 ,前
,前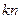 项和记为
项和记为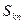
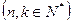 ,对给定的常数
,对给定的常数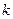 ,若
,若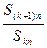 是与
是与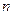 无关的非零常数
无关的非零常数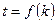 ,则称该数列
,则称该数列 是“
是“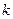 类和科比数列”,
类和科比数列”,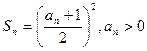 ,求数列
,求数列 的通项公式(5分);
的通项公式(5分);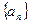 是一个 “
是一个 “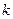 类和科比数列”(4分);
类和科比数列”(4分);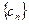 是一个等比数列,首项
是一个等比数列,首项 ,公比
,公比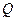
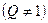 ,若数列
,若数列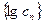 是一个 “
是一个 “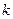 类和科比数列”,探究
类和科比数列”,探究 与
与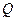 的关系(7分)
的关系(7分)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com