
分析 (1)将x=0,x=-1带入直接计算.
(2)利用定义在R的偶函数,f(-x)=f(x)即可求解.
(3)对a的范围分段讨论计算.
解答 解:(1)∵当x≥0时,$f(x)={log_{\frac{1}{2}}}(x+1)$.∴f(0)=0.
f(x)是定义在R的偶函数,f(-1)=f(1),
f(1)=$lo{g}_{\frac{1}{2}}(1+1)$=-1.
∴f(-1)=-1.
(2)f(x)是定义在R的偶函数,当x<0时,则-x>0,
∴f(x)=f(-x)=$lo{g}_{\frac{1}{2}}(-x+1)$
故f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(x+1),(x≥0)}\\{lo{g}_{\frac{1}{2}}(-x+1),(x<0)}\end{array}\right.$
(3)由偶函数的区间对称性的单调性具有相反性,可得:$f(x)={log_{\frac{1}{2}}}(x+1)$在区间[0,+∞)是减函数,在(-∞,0)是增函数.
由于f(a-1)<f(3-a),所以:|a-1|>|3-a|.
解得:a>2.
点评 本题考查了函数的奇偶性和对数函数的单调性的综合运用,还考查了分段函数的解析式以及转化思想.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
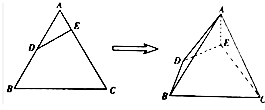 如图,已知△ABC为正三角形,D为AB的中点,E在AC上,且AE
如图,已知△ABC为正三角形,D为AB的中点,E在AC上,且AE查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
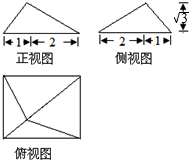 某四棱锥的三视图如图所示(单位:cm),则该四棱锥的表面积是( )
某四棱锥的三视图如图所示(单位:cm),则该四棱锥的表面积是( )| A. | $(13+3\sqrt{7})c{m^2}$ | B. | $(12+4\sqrt{3})c{m^2}$ | C. | $(18+3\sqrt{7})c{m^2}$ | D. | $(15+3\sqrt{7})c{m^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com