
【题目】已知函数![]() ,
,![]() 是
是![]() 的导函数。
的导函数。
(1)证明:![]() 在
在![]() 内存在唯一的极小值点;
内存在唯一的极小值点;
(2)证明:当![]() 时,
时,![]() 有且只有两个零点.
有且只有两个零点.
【答案】(1)见解析;(2)见解析.
【解析】
(1)令![]() ,可知函数
,可知函数![]() 在
在![]() 单调递增,利用零点存在定理并结合函数
单调递增,利用零点存在定理并结合函数![]() 在
在![]() 上的单调性可证明出函数
上的单调性可证明出函数![]() 在
在![]() 内存在唯一的极小值点;
内存在唯一的极小值点;
(2)利用导数证明出函数![]() 在区间
在区间![]() 上为增函数,结合零点存在定理可证明出函数
上为增函数,结合零点存在定理可证明出函数![]() 在区间
在区间![]() 只有一个零点,利用(1)中的结论可证明出函数
只有一个零点,利用(1)中的结论可证明出函数![]() 在区间
在区间![]() 上没有零点,再由
上没有零点,再由![]() 以及函数
以及函数![]() 在
在![]() 上单调递增,可证明出函数
上单调递增,可证明出函数![]() 有且只有两个零点.
有且只有两个零点.
(1)令![]() ,则
,则![]() ,
,
显然函数![]() 在
在![]() 单调递增.
单调递增.
因为![]() ,
,![]() ,
,
(因为![]() )
)
故存在唯一的![]() 使得
使得![]() .
.
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
所以函数![]() ,即
,即![]() 在区间
在区间![]() 存在唯一的极小值点
存在唯一的极小值点![]() ,且
,且![]() ;
;
(2)当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,![]() ,
,![]() ,
,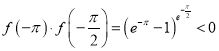 ,
,
所以,函数![]() 在区间
在区间![]() 上存在唯一的零点.
上存在唯一的零点.
当![]() 时,由(1)当
时,由(1)当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,![]() ,
,![]() ,所以存在
,所以存在![]() ,使得
,使得![]() ,
,
当![]() ,
,![]() ,当
,当![]() ,
,![]() ,
,
所以![]() 在
在![]() 先递增后递减,
先递增后递减,![]() ,
,![]() ,
,
函数![]() 在
在![]() 没有零点;
没有零点;
因为![]() ,所以
,所以![]() 是函数
是函数![]() 的第二个零点;
的第二个零点;
![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,![]() ,没有零点.
,没有零点.
综上所述,当![]() 时,函数
时,函数![]() 有且只有两个零点.
有且只有两个零点.


科目:高中数学 来源: 题型:
【题目】若数列![]() 同时满足条件:①存在互异的
同时满足条件:①存在互异的![]() 使得
使得![]() (
(![]() 为常数);
为常数);
②当![]() 且
且![]() 时,对任意
时,对任意![]() 都有
都有![]() ,则称数列
,则称数列![]() 为双底数列.
为双底数列.
(1)判断以下数列![]() 是否为双底数列(只需写出结论不必证明);
是否为双底数列(只需写出结论不必证明);
①![]() ; ②
; ②![]() ; ③
; ③![]()
(2)设![]() ,若数列
,若数列![]() 是双底数列,求实数
是双底数列,求实数![]() 的值以及数列
的值以及数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() ,是否存在整数
,是否存在整数![]() ,使得数列
,使得数列![]() 为双底数列?若存在,求出所有的
为双底数列?若存在,求出所有的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
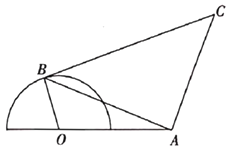
【题目】某生态农庄有一块如图所示的空地,其中半圆O的直径为300米,A为直径延长线上的点,![]() 米,B为半圆上任意一点,以AB为一边作等腰直角
米,B为半圆上任意一点,以AB为一边作等腰直角![]() ,其中BC为斜边.
,其中BC为斜边.
![]() 若
若![]() ;,求四边形OACB的面积;
;,求四边形OACB的面积;
![]() 现决定对四边形OACB区域地块进行开发,将
现决定对四边形OACB区域地块进行开发,将![]() 区域开发成垂钓中心,预计每平方米获利10元,将
区域开发成垂钓中心,预计每平方米获利10元,将![]() 区域开发成亲子采摘中心,预计每平方米获利20元,则当
区域开发成亲子采摘中心,预计每平方米获利20元,则当![]() 为多大时,垂钓中心和亲子采摘中心获利之和最大?
为多大时,垂钓中心和亲子采摘中心获利之和最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
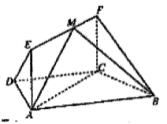
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,且
为矩形,且![]() 平面
平面![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,当点
上运动,当点![]() 在什么位置时,平面
在什么位置时,平面![]() 与平面
与平面![]() 所成锐二面角最大,并求此时二面角的余弦值.
所成锐二面角最大,并求此时二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2011年国际数学协会正式宣布,将每年的3月14日设为国际数学节,来源于中国古代数学家祖冲之的圆周率。公元263年,中国数学家刘徽用“割圆术”计算圆周率,计算到圆内接3072边形的面积,得到的圆周率是![]() .公元480年左右,南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果,给出不足近似值3.1415926和过剩近似值3.1415927,还得到两个近似分数值,密率
.公元480年左右,南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果,给出不足近似值3.1415926和过剩近似值3.1415927,还得到两个近似分数值,密率![]() 和约率
和约率![]() 。大约在公元530年,印度数学大师阿耶波多算出圆周率约为
。大约在公元530年,印度数学大师阿耶波多算出圆周率约为![]() (
(![]() ).在这4个圆周率的近似值中,最接近真实值的是( )
).在这4个圆周率的近似值中,最接近真实值的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知曲线![]() :
:![]() 和曲线
和曲线![]() :
:![]() ,以极点
,以极点![]() 为坐标原点,极轴为
为坐标原点,极轴为![]() 轴非负半轴建立平面直角坐标系.
轴非负半轴建立平面直角坐标系.
(1)求曲线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 是曲线
是曲线![]() 上一动点,过点
上一动点,过点![]() 作线段
作线段![]() 的垂线交曲线
的垂线交曲线![]() 于点
于点![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥S﹣ABCD的底面为矩形,SA⊥底面ABCD,点E在线段BC上,以AD为直径的圆过点 E.若SA=![]() AB=3,则△SED面积的最小值为_____.
AB=3,则△SED面积的最小值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的一个顶点与抛物线
的一个顶点与抛物线![]() 的焦点重合,
的焦点重合,![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,其离心率
的左、右焦点,其离心率![]() 椭圆
椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com