
| A. | $(-3,-\sqrt{6})$ | B. | $(-2,-\sqrt{3})$ | C. | [-2,1) | D. | (-2,1) |
分析 由给出的是开区间,且给的函数只有一个极大值点,可得最大值一定是在该极大值点处取得,因此对原函数求导、求极大值点,然后让极大值点落在区间(t,10-t2)内,由此构造不等式组求解.
解答 解:由$f(x)=-\frac{1}{3}{x}^{3}+x$,得f′(x)=-x2+1,
由f′(x)=0,得x=±1.
当x∈(-∞,-1)∪(1,+∞)时,f′(x)<0,
∴f(x)的减区间为(-∞,-1),(1,+∞);
当x∈(-1,1)时,f′(x)>0,
∴f(x)的增区间为(-1,1).
∴x=1时,f(x)取得极大值,
要使函数f(x)=$-\frac{1}{3}{x}^{3}+x$在(t,10-t2)上有最大值,
则$\left\{\begin{array}{l}{t<1<10-{t}^{2}}\\{f(t)≤f(1)}\end{array}\right.$,即$\left\{\begin{array}{l}{t<1<10-{t}^{2}}\\{-\frac{1}{3}{t}^{3}+t≤\frac{2}{3}}\end{array}\right.$,
解得:-2≤t<1.
∴实数t的取值范围为[-2,1).
故选:C.
点评 本题考查利用导数求函数在闭区间上的最值,考查数学转化思想方法,属中档题.


科目:高中数学 来源: 题型:选择题

| A. | 24+8$\sqrt{2}$+8$\sqrt{5}$ | B. | 20+8$\sqrt{2}$+4$\sqrt{5}$ | C. | 20+8$\sqrt{5}$+4$\sqrt{2}$ | D. | 20+4$\sqrt{2}$+4$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
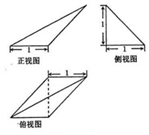
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
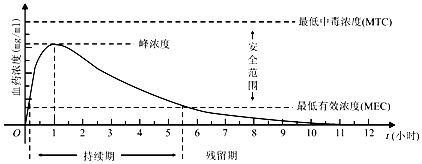
| A. | 首次服用该药物1单位约10分钟后,药物发挥治疗作用 | |
| B. | 每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒 | |
| C. | 每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用 | |
| D. | 首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com