
| A�� | �״η��ø�ҩ��1��λԼ10���Ӻ�ҩ����������� | |
| B�� | ÿ�η��ø�ҩ��1��λ�����η�ҩ���С��2Сʱ��һ�������ҩ���ж� | |
| C�� | ÿ���5.5Сʱ���ø�ҩ��1��λ����ʹҩ����������������� | |
| D�� | �״η��ø�ҩ��1��λ3Сʱ���ٴη��ø�ҩ��1��λ�����ᷢ��ҩ���ж� |
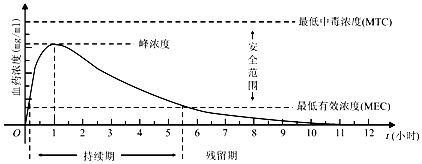
���� ����ͼ�����ۼ�Ũ���Ƿ�����ж�Ũ�ȣ������жϳ��Ƿ�ᷢ��ҩ���ж��������жϳ����ۣ�
��� �⣺��ͼ���֪��
A���״η��ø�ҩ��1��λԼ10���Ӻ�ҩ����������ã���ȷ��
B��ÿ�η��ø�ҩ��1��λ�����η�ҩ���С��2Сʱ����߷�ֵ�ᳬ������ж�Ũ�ȣ����һ�������ҩ���ж���
C��ÿ���5.5Сʱ���ø�ҩ��1��λ����ʹҩ����������������ã���ȷ��
D���״η��ø�ҩ��1��λ3Сʱ���ٴη��ø�ҩ��1��λ���ۼ�Ũ�Ȼᳬ������ж�Ũ�ȣ��ᷢ��ҩ���ж�����˲���ȷ��
��ѡ��D��
���� ���⿼���˺�����ͼ�������ʡ����ν�Ϸ���������������������������������ڻ����⣮


 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��2����e2f��0����f��2001����e2001f��0�� | B�� | f��2����e2f��0����f��2001����e2001f��0�� | ||
| C�� | f��2����e2f��0����f��2001����e2001f��0�� | D�� | f��2����e2f��0����f��2001����e2001f��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��-3��-\sqrt{6}��$ | B�� | $��-2��-\sqrt{3}��$ | C�� | [-2��1�� | D�� | ��-2��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4��6 | B�� | 3��6 | C�� | 3��7 | D�� | 1��7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
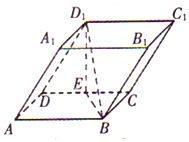 ��ͼ����������ABCD-A1B1C1D1�У�����ABCD�Ͳ���BCC1B1���Ǿ��Σ�E��CD���е㣬D1E��CD��AB=2BC=2��
��ͼ����������ABCD-A1B1C1D1�У�����ABCD�Ͳ���BCC1B1���Ǿ��Σ�E��CD���е㣬D1E��CD��AB=2BC=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �������������У���������ֱ�������ε�ֱ��������Ϊ��ǵ�¡�����֪ij��ǵ�¡�������ͼ��ͼ��ʾ������ͼ������ƽ�־��ε��������á�ǵ�¡����������Ϊ$\frac{8\sqrt{2}��}{3}$��
�������������У���������ֱ�������ε�ֱ��������Ϊ��ǵ�¡�����֪ij��ǵ�¡�������ͼ��ͼ��ʾ������ͼ������ƽ�־��ε��������á�ǵ�¡����������Ϊ$\frac{8\sqrt{2}��}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com