
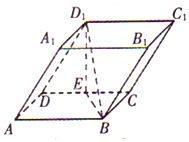
 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.分析 (1)由已知底面ABCD和侧面BCC1B1是矩形,可得BC⊥CD,BC⊥CC1,由线面垂直的判定可得BC⊥平面DCC1D1,进一步得到BC⊥D1E;
(2)由(1)可知BC⊥D1E,结合D1E⊥CD,可得D1E⊥平面ABCD.设G为AB的中点,以E为原点,EG,EC,ED1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,求出平面BED1的一个法向量与平面BCC1B1的一个法向量,由平面BCC1B1与平面BED1所成的锐二面角的大小为$\frac{π}{3}$列式求得a值,则线段D1E的长度可求.
解答 (1)证明:∵底面ABCD和侧面BCC1B1是矩形,∴BC⊥CD,BC⊥CC1,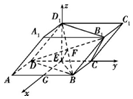
又∵CD∩CC1=C,∴BC⊥平面DCC1D1,
∵D1E?平面DCC1D1,∴BC⊥D1E;
(2)解:由(1)可知BC⊥D1E,
又∵D1E⊥CD,且BC∩CD=C,
∴D1E⊥平面ABCD.
设G为AB的中点,以E为原点,EG,EC,ED1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图.
则E(0,0,0),B(1,1,0),C(0,1,0),G(1,0,0).
设D1E=a,则D1(0,0,a),B1(1,2,a).
设平面BED1的一个法向量为$\overrightarrow{n}$=(x,y,z),
$\overrightarrow{EB}$=(1,1,0),$\overrightarrow{E{D}_{1}}$=(0,0,a),
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EB}=x+y=0}\\{\overrightarrow{n}•\overrightarrow{E{D}_{1}}=az=0}\end{array}\right.$,令x=1,得$\overrightarrow{n}$=(1,-1,0);
设平面BCC1B1的一个法向量为$\overrightarrow{m}$=(x1,y1,z1),
$\overrightarrow{CB}$=(1,0,0),$\overrightarrow{B{C}_{1}}$=(-1,1,a),
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{CB}={x}_{1}=0}\\{\overrightarrow{m}•\overrightarrow{B{C}_{1}}=-{x}_{1}+{y}_{1}+a{z}_{1}=0}\end{array}\right.$,令z1=1,得$\overrightarrow{m}$=(0,-a,1).
由平面BCC1B1与平面BED1所成的锐二面角的大小为$\frac{π}{3}$,
得|cos<$\overrightarrow{m},\overrightarrow{n}$>|=|$\frac{a}{\sqrt{2}•\sqrt{{a}^{2}+1}}$=|cos$\frac{π}{3}$=$\frac{1}{2}$,解得a=1.
∴D1E=1.
点评 本题考查空间中直线与直线的位置关系,考查空间想象能力和思维能力,训练了利用空间向量求解二面角的平面角,是中档题.


科目:高中数学 来源: 题型:解答题
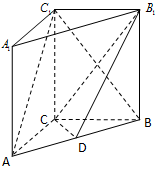 如图,在三棱柱ABC-A1B1C1中侧棱垂直于底面,AC⊥BC,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中侧棱垂直于底面,AC⊥BC,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 24+8$\sqrt{2}$+8$\sqrt{5}$ | B. | 20+8$\sqrt{2}$+4$\sqrt{5}$ | C. | 20+8$\sqrt{5}$+4$\sqrt{2}$ | D. | 20+4$\sqrt{2}$+4$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
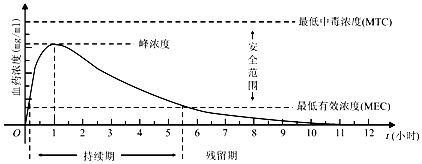
| A. | 首次服用该药物1单位约10分钟后,药物发挥治疗作用 | |
| B. | 每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒 | |
| C. | 每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用 | |
| D. | 首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”其意思为:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈,上棱长2丈,无宽,高1丈.现给出该楔体的三视图,其中网格纸上小正方形的边长为1丈,则该楔体的体积为( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”其意思为:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈,上棱长2丈,无宽,高1丈.现给出该楔体的三视图,其中网格纸上小正方形的边长为1丈,则该楔体的体积为( )| A. | 4立方丈 | B. | 5立方丈 | C. | 6立方丈 | D. | 8立方丈 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com