
分析 (1)根据正弦定理和两角和的正弦公式,根据特殊角的三角函数值即可求出,
(2)根据余弦定理求出b即可
解答 解:(1)因为(2a-c)cos B=bcos C,由正弦定理,得
(2sin A-sin C)cos B=sin Bcos C,
即2sin Acos B=sin Ccos B+sin Bcos C=sin(C+B)=sin A.
在△ABC中,0<A<π,sin A>0,
所以cos B=$\frac{1}{2}$.
又因为0<B<π,
故B=$\frac{π}{3}$.
(2)因为$a=c=\sqrt{3}$,由余弦定理得b2=a2+c2-2accos B,
所以b2=3.
所以$b=\sqrt{3}$.
点评 本题考查正余弦定理的应用,涉及三角函数的恒等变形,关键是熟悉三角函数的恒等变形的公式.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:选择题
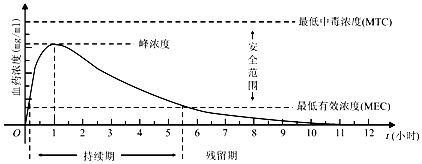
| A. | 首次服用该药物1单位约10分钟后,药物发挥治疗作用 | |
| B. | 每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒 | |
| C. | 每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用 | |
| D. | 首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
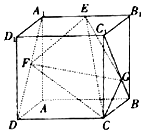 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为线段A1B1的中点,点F,G分别是线段A1D与BC1上的动点,当三棱锥E-FGC的俯视图的面积最大时,该三棱锥的正视图的面积是2.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为线段A1B1的中点,点F,G分别是线段A1D与BC1上的动点,当三棱锥E-FGC的俯视图的面积最大时,该三棱锥的正视图的面积是2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com