
| A. | f(2)>e2f(0),f(2001)>e2001f(0) | B. | f(2)<e2f(0),f(2001)>e2001f(0) | ||
| C. | f(2)>e2f(0),f(2001)<e2001f(0) | D. | f(2)<e2f(0),f(2001)<e2001f(0) |
分析 构造函数g(x)=$\frac{f(x)}{{e}^{x}}$,利用导数判断函数g(x)的单调性,通过单调性得到答案.
解答 解:设g(x)=$\frac{f(x)}{{e}^{x}}$,
∴g′(x)=$\frac{f′(x)-f(x)}{{e}^{x}}$,
∵f'(x)<f(x),
∴g′(x)<0,
∴g(x)在R上递减,
∴g(0)>g(2),g(0)>g(2011),
∴f(0)>$\frac{f(2)}{{e}^{2}}$,f(0)>$\frac{f(2001)}{{e}^{2001}}$,
∴f(2)<e2f(0),f(2001)<e2001f(0),
故选:D
点评 本题考查了函数的单调性和导数的关系,关键是构造函数,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 24+8$\sqrt{2}$+8$\sqrt{5}$ | B. | 20+8$\sqrt{2}$+4$\sqrt{5}$ | C. | 20+8$\sqrt{5}$+4$\sqrt{2}$ | D. | 20+4$\sqrt{2}$+4$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
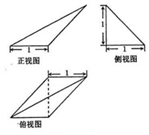
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
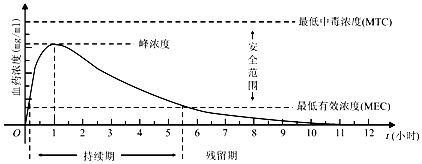
| A. | 首次服用该药物1单位约10分钟后,药物发挥治疗作用 | |
| B. | 每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒 | |
| C. | 每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用 | |
| D. | 首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com