
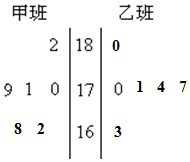
 随机抽取某中学甲乙两班各6名学生,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
随机抽取某中学甲乙两班各6名学生,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.分析 (1)由茎叶图知乙班同学的身高较高.
(2)先求出$\overline{{x}_{甲}}$,再求${{{S}_{甲}}^{2}}_{\;}$,由此能求出甲班的样本方差.
(3)至少有一名身高不低于175cm的学生被抽中的对立事件是抽中的两名同学的身高都低于175cm,由此利用对立事件概率计算公式能求出至少有一名身高不低于175cm的学生被抽中的概率.
解答 解:(1)由茎叶图知乙班同学的身高较高.
理由是甲班的同学身高数值位于茎叶图的左下方,乙班同学身高数值位于茎叶图的中间,
本茎叶图中数值越靠上越大.
(2)$\overline{{x}_{甲}}$=$\frac{1}{6}$[(182+171+170+179+162+168)]=172,
${{{S}_{甲}}^{2}}_{\;}$=$\frac{1}{6}$[(182-172)2+(171-172)2+(180-172)2+(179-172)2+(162-172)2+(168-172)2]=55.
∴甲班的样本方差为55.
(3)现从乙班这6名学生中随机抽取两名学生,
基本事件总数n=${C}_{6}^{2}=15$,
至少有一名身高不低于175cm的学生被抽中的对立事件是抽中的两名同学的身高都低于175cm,
∴至少有一名身高不低于175cm的学生被抽中的概率p=1-$\frac{{C}_{4}^{2}}{{C}_{6}^{2}}$=$\frac{3}{5}$.
点评 本题考查茎叶图的应用,考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率公式的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M>N | B. | M<N | C. | M≥N | D. | M≤N |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
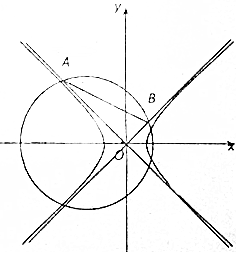 如图,双曲线k2x2-y2=1(k>0)的两条渐近线与圆(x+2)2+y2=5在x轴的上方交于A、B两点.
如图,双曲线k2x2-y2=1(k>0)的两条渐近线与圆(x+2)2+y2=5在x轴的上方交于A、B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com