练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．已知lg2=n，lg3=m，则${lg^{\frac{2}{3}}}$=（　　）
    A．n+mB．n-mC．2n+mD．2n-m

    分析 利用对数性质、运算法则求解．

    解答 解：∵lg2=n，lg3=m，
    ∴${lg^{\frac{2}{3}}}$=lg2-lg3=n-m．
    故选：B．

    点评 本题考查对数式化简求值，是基础题，解题时要认真审题，注意对数性质、运算法则的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    7．定义平面向量之间的一种运算“⊙“如下：对任意的向量$\overrightarrow{a}$=（m，n），$\overrightarrow{b}$=（p，q）（其中m，n，p，q均为实数），$\overrightarrow{a}$⊙$\overrightarrow{b}$=mq-np．在下列说法中：
    （1）若向量与$\overrightarrow{b}$共线，则$\overrightarrow{a}$⊙$\overrightarrow{b}$=0；
    （2）$\overrightarrow{a}$⊙$\overrightarrow{b}$=$\overrightarrow{b}$⊙$\overrightarrow{a}$；
    （3）对任意；
    （4）（$\overrightarrow{a}$⊙$\overrightarrow{b}$）2+（$\overrightarrow{a}$•$\overrightarrow{b}$）2=|$\overrightarrow{a}$|2|$\overrightarrow{b}$|2（其中$\overrightarrow{a}$•$\overrightarrow{b}$表示与$\overrightarrow{b}$的数量积，|$\overrightarrow{a}$|表示向量的模）．
    正确的说法是（1）（3）（4）．（写出所有正确的说法的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

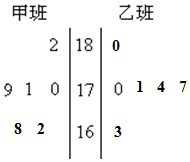    8．随机抽取某中学甲乙两班各6名学生，测量他们的身高（单位：cm），获得身高数据的茎叶图如图．
    （1）判断哪个班的平均身高较高，并说明理由；
    （2）计算甲班的样本方差；
    （3）现从乙班这6名学生中随机抽取两名学生，求至少有一名身高不低于175cm的学生被抽中的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．如图，在△ABC中，∠C=Rt∠，以顶点C为圆心，BC为半径作圆．若$AC=4，tanA=\frac{3}{4}$求AB的长度为5；⊙C截AB所得弦BD的长为$\frac{18}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

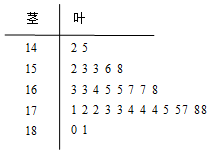    12．从某校的高一学生中采用系统抽样法选出30人测量其身高，数据的茎叶图如图（单位：cm）：若高一年级共有600人，据上图估算身高在1.70m以上的大约有300人．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知二项分布满足X～B（6，$\frac{2}{3}$），则P（X=2）=$\frac{20}{243}$，E（X）=4，D（x）=$\frac{4}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知命题p：方程ax2+ax-2=0在[-1，1]上有解，命题q：只有一个实数x满足：x2+2ax+2a≤0．
    （Ⅰ）若f（x）=ax2+ax-2，则f（x）的图象必定过两定点，试写出这两定点的坐标（-1，-2），（0，-2）（只需填写出两点坐标即可）；
    （Ⅱ）若命题“p或q”为假命题，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．现安排甲、乙、丙、丁4名同学参加上海世博会志愿者服务活动，每人从事翻译、导游、礼仪、司机四项工作之一，每项工作都有一人参加．甲、乙不会开车但能从事其他三项工作，丙、丁都能胜任四项工作，则不同安排方案的种数为12 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．二次函数f（x）的图象顶点为A（1，16），且图象在x轴上截得线段长为8．
    （1）求函数f（x）的解析式；
    （2）令g（x）=f（x）+（2a-2）x，求函数g（x）在x∈[0，2]的最大值．

    查看答案和解析>>

    同步练习册答案