
分析 (Ⅰ)由f(x)=ax2+ax-2=a(x2+x)-2的图象必定过两定点,可知x2+x=0且y=-2,从而可写出这两定点的坐标(只需填写出两点坐标即可);
(Ⅱ)若命题“p或q”为假命题,命题p、q均为假命题,分别求得a的取值范围,再取交集即可求得实数a的取值范围.
解答 解:(Ⅰ)f(x)=ax2+ax-2,则f(x)的图象必定过两定点,这两定点的坐标为(-1,-2),(0,-2);
(Ⅱ)因为命题“p或q”为假命题,所以命题p、q均为假命题.
因为方程ax2+ax-2=0在[-1,1]上无解,f(x)的图象过定点(-1,-2),(0,-2)
所以a=0或$\left\{\begin{array}{l}a>0\\ f(1)<0\end{array}\right.或\left\{\begin{array}{l}a<0\\△={a^2}+8a<0\end{array}\right.$,
即a=0或0<a<1或-8<a<0,∴-8<a<1;
又∵命题q不成立的条件是:△=4a2-8a≠0⇒a≠0且a≠2;
所以-8<a<0或0<a<1.
故(Ⅰ)的答案为:(-1,-2),(0,-2).
点评 本题考查命题的真假判断与应用,考查二次函数过定点问题与二次函数的性质,考查分析问题、解决问题的能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
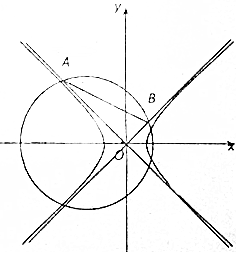 如图,双曲线k2x2-y2=1(k>0)的两条渐近线与圆(x+2)2+y2=5在x轴的上方交于A、B两点.
如图,双曲线k2x2-y2=1(k>0)的两条渐近线与圆(x+2)2+y2=5在x轴的上方交于A、B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 45°或135° | C. | 30° | D. | 30°或150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | [$\frac{1}{2}$,1] | C. | [$\frac{1}{2}$,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (1,2] | C. | [1,2] | D. | (1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com