
| A. | [0,+∞) | B. | [$\frac{1}{2}$,1] | C. | [$\frac{1}{2}$,+∞) | D. | [1,+∞) |
分析 对a讨论,分a≤0,a>0,可得a>0成立,由|x2-a|=a,可得x=0或±$\sqrt{2a}$,由$\sqrt{2a}$≥1,即可得到所求范围.
解答 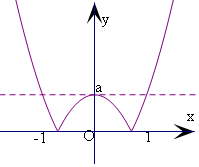 解:若a≤0,则f(x)=x2-a,
解:若a≤0,则f(x)=x2-a,
f(x)在[-1,1]的最大值为1-a,
即有1-a=a,可得a=$\frac{1}{2}$,不成立;
则a>0,由|x2-a|=a,可得x=0或±$\sqrt{2a}$,
由图象结合在区间[-1,1]上的最大值是a,
可得$\sqrt{2a}$≥1,解得a≥$\frac{1}{2}$.
故选:C.
点评 本题考查函数的最值的判断,考查分类讨论思想方法,数形结合思想,以及运算能力,属于中档题.


 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源: 题型:填空题
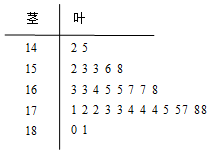 从某校的高一学生中采用系统抽样法选出30人测量其身高,数据的茎叶图如图(单位:cm):若高一年级共有600人,据上图估算身高在1.70m以上的大约有300人.
从某校的高一学生中采用系统抽样法选出30人测量其身高,数据的茎叶图如图(单位:cm):若高一年级共有600人,据上图估算身高在1.70m以上的大约有300人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8<a<10 | B. | 2$\sqrt{2}<a<\sqrt{10}$ | C. | $2\sqrt{2}<a<10$ | D. | $\sqrt{10}<a<8$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<c<a | C. | a<c<b | D. | c<a<b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com