
【题目】已知命题![]() ,
,![]() ;命题
;命题![]() 关于
关于![]() 的方程
的方程![]() 有两个相异实数根.
有两个相异实数根.
(1)若![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 为真命题,
为真命题,![]() 为假命题,求实数
为假命题,求实数![]() 的取值范围.
的取值范围.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
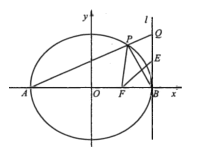
【题目】在平面直角坐标系xOy中,己知椭圆C:![]() 的左、右顶点为A,B,右焦点为F.过点A且斜率为k(
的左、右顶点为A,B,右焦点为F.过点A且斜率为k(![]() )的直线交椭圆C于另一点P.
)的直线交椭圆C于另一点P.
(1)求椭圆C的离心率;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)设直线l:![]() ,延长AP交直线l于点Q,线段BO的中点为E,求证:点B关于直线EF的对称点在直线PF上。
,延长AP交直线l于点Q,线段BO的中点为E,求证:点B关于直线EF的对称点在直线PF上。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区不同身高![]() 的未成年男孩的体重平均值
的未成年男孩的体重平均值![]() 如下表:
如下表:
身高 | 60 | 70 | 80 | 90 | 100 |
体重 | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 |
已知![]() 与
与![]() 之间存在很强的线性相关性,
之间存在很强的线性相关性,
(1)据此建立![]() 与
与![]() 之间的回归方程;
之间的回归方程;
(2)若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高![]() 体重为
体重为![]() 的在校男生的体重是否正常?
的在校男生的体重是否正常?
参考数据:![]() ,
,![]() ,
,![]()
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 下列结论错误的是
A. 命题:“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() ”
”
B. “![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C. 命题:“![]() ,
, ![]() ”的否定是“
”的否定是“![]() ,
, ![]() ”
”
D. 若“![]() ”为假命题,则
”为假命题,则![]() 均为假命题
均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】到2020年,我国将全面建立起新的高考制度,新高考采用![]() 模式,其中语文、数学、英语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣、爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门(6选3)参加考试,满分各100分.为了顺利迎接新高考改革,某学校采用分层抽样的方法从高一年级1000名(其中男生550名,女生450名)学生中抽取了
模式,其中语文、数学、英语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣、爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门(6选3)参加考试,满分各100分.为了顺利迎接新高考改革,某学校采用分层抽样的方法从高一年级1000名(其中男生550名,女生450名)学生中抽取了![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中有女生45名,求
名学生中有女生45名,求![]() 的值及抽取的男生的人数.
的值及抽取的男生的人数.
(2)该校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目,且只能选择一个科目),得到如下
名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目,且只能选择一个科目),得到如下![]() 列联表.
列联表.
选择“物理” | 选择“地理” | 总计 | |
男生 | 10 | ||
女生 | 25 | ||
总计 |
(i)请将列联表补充完整,并判断是否有![]() 以上的把握认为选择科目与性别有关系.
以上的把握认为选择科目与性别有关系.
(ii)在抽取的选择“地理”的学生中按性别分层抽样抽取6名,再从这6名学生中抽取2名,求这2名中至少有1名男生的概率.
附:![]() ,其中
,其中![]() .
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 上位于第一象限内的任意一点,
上位于第一象限内的任意一点,![]() 为坐标原点,
为坐标原点,![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,![]() ,圆
,圆![]() :
:![]() .
.

(1)求椭圆![]() 和圆
和圆![]() 的标准方程;
的标准方程;
(2)过点![]() 作
作![]() 与圆
与圆![]() 相切于点
相切于点![]() ,使得点
,使得点![]() ,点
,点![]() 在
在![]() 的两侧.求四边形
的两侧.求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,平面
为平行四边形,平面![]() 平面
平面![]() ,
,![]() 是边长为4的等边三角形,
是边长为4的等边三角形,![]() ,
,![]() 是
是![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求平面
,求平面 ![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com