
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,平面
为平行四边形,平面![]() 平面
平面![]() ,
,![]() 是边长为4的等边三角形,
是边长为4的等边三角形,![]() ,
,![]() 是
是![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求平面
,求平面 ![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
【答案】(1)见证明;(2) ![]()
【解析】
(1)由面面垂直的性质可得![]() 平面
平面![]() .可得
.可得![]() ,
,![]() ,结合
,结合![]() 得
得![]() 平面
平面![]() .由
.由![]() ,可得
,可得![]() ,得到
,得到![]() 平面
平面![]() ,从而可得结果;(2)根据直线
,从而可得结果;(2)根据直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,可求得
,可求得![]() ,
, ![]() ,以
,以![]() ,
,![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系,利用向量垂直数量积为零列方程求出平面
轴,建立空间直角坐标系,利用向量垂直数量积为零列方程求出平面![]() 的一个法向量,结合平面
的一个法向量,结合平面![]() 的一个法向量为
的一个法向量为![]() ,利用空间向量夹角余弦公式可得结果.
,利用空间向量夹角余弦公式可得结果.
(1)因为![]() 是等边三角形,
是等边三角形,![]() 是
是![]() 的中点,
的中点,
所以![]() .
.
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
所以![]() ,
,![]()
又因为![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .所以
.所以![]() .
.
又因为![]() ,所以
,所以![]() .
.
又![]() 且
且![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
所以![]() .
.
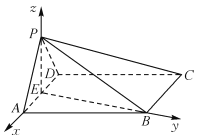
(2)
由(1)得![]() 平面
平面![]() .
.
所以![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成角.
所成角.
因为直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,即
,即![]() ,所以
,所以![]() .
.
所以![]() ,解得
,解得![]() .则
.则![]() .
.
由(1)得![]() ,
,![]() ,
,![]() 两两垂直,所以以
两两垂直,所以以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() ,
,![]() ,
,![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
则点![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
令平面![]() 的法向量为
的法向量为![]() ,则
,则
由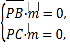 得
得![]() 解得
解得![]()
令![]() ,可得平面
,可得平面![]() 的一个法向量为
的一个法向量为![]() ;
;
易知平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设平面![]() 与平面
与平面![]() 所成的锐二面角的大小为
所成的锐二面角的大小为![]() ,则
,则![]() .
.
所以平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .
.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在四棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 的中点.
的中点.

(1)证明:![]() ;
;
(2)求二面角![]() 的平面角的正弦值;
的平面角的正弦值;
(3)设点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的检验员为了检测生产线上生产零件的情况,从产品中随机抽取了![]() 个进行测量,根据所测量的数据画出频率分布直方图如下:
个进行测量,根据所测量的数据画出频率分布直方图如下:

如果:尺寸数据在![]() 内的零件为合格品,频率作为概率.
内的零件为合格品,频率作为概率.
(1)从产品中随机抽取![]() 件,合格品的个数为
件,合格品的个数为![]() ,求
,求![]() 的分布列与期望:
的分布列与期望:
(2)为了提高产品合格率,现提出![]() ,
,![]() 两种不同的改进方案进行试验,若按
两种不同的改进方案进行试验,若按![]() 方案进行试验后,随机抽取
方案进行试验后,随机抽取![]() 件产品,不合格个数的期望是
件产品,不合格个数的期望是![]() :若按
:若按![]() 方案试验后,抽取
方案试验后,抽取![]() 件产品,不合格个数的期望是
件产品,不合格个数的期望是![]() ,你会选择哪个改进方案?
,你会选择哪个改进方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信抢红包”自2015年以来异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为10元,被随机分配为1元,2.5元,3元,3.5元,共4份,供甲、乙等4人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于6元的概率是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com