练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．函数y=e|lnx|的图象大致为（　　）
    A．B．C．D．

    分析 根据复合函数的单调性即可判断．

    解答 解：因为t=|lnx|=$\left\{\begin{array}{l}{ln\frac{1}{x}，0＜x＜1}\\{lnx，x≥1}\end{array}\right.$，
    当0＜x＜1时，函数y=|lnx|为减函数，
    当x≤1时，函数y=|lnx|为增函数，
    又因为y=ex为增函数，
    所以y=e|lnx|在（0，1）上为减函数，在[1，+∞）为增函数，
    故选：A．

    点评 本题考查了复合函数的单调性以及绝对值函数的图象和性质，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．求y=|x+10|+|x-14|+|x-3|的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．函数f（x）=$\frac{3}{lgx-1}$的定义域为{x|x＞0，且x≠10}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

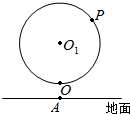    11．如图，某大风车的半径为2米，每12秒旋转一周，它的最低点O离地面1米，点O在地面上的射影为A．风车圆周上一点M从最低点O开始，逆时针方向旋转40秒后到达P点，则点P到点A的距离与点P的高度之和为（　　）
    A．5B．4$+\sqrt{7}$C．4$+\sqrt{17}$D．4$+\sqrt{19}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．在直角坐标系xOy中，曲线C的参数方程是$\left\{\begin{array}{l}{x=2cosθ}\\{y=\sqrt{3}sinθ}\end{array}\right.$（θ是参数），以坐标原点为极点，x轴的正半轴为极轴，建立极坐标系，直线l的极坐标方程是$\sqrt{2}$ρsin（θ-$\frac{π}{4}$）=1．
    （1）求曲线C的普通方程和直线l的直角坐标方程；
    （2）设曲线C和直线l相交于点M，N，试求出过M，N两点的圆中面积最小的圆的标准方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．某企业生产A、B两种产品，根据市场调查与市场预测，A产品的利润与投资成正比，其关系如图（1）；B产品的利润与投资的算术平方根成正比，其关系如图（2）（注：所示图中的横坐标表示投资金额，单位为万元）

    （1）分别求出A、B两种产品的利润表示为投资的函数关系式；
    （2）该企业已筹集到10万元资金，并全部投入A、B两种产品的生产，问：怎样分配这10万元资金，才能使企业获得最大利润，最大利润是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知函数$f（x）=\left\{\begin{array}{l}x+2，x≤0\\ 1gx，x＞0\end{array}\right.$，则函数y=|f（x）|-1的零点个数是（　　）
    A．1B．4C．3D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．如图，在三棱柱ABC-A1B1C1中，AA1⊥平面ABC，∠ACB=90°，CA=CB=CC1=1，则直线A1B与平面BB1C1C所成角的正弦值为$\frac{\sqrt{3}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．某学校随机抽取部分新生调查其上学路上所需时间（单位：分钟），并将所得数据制成频率分布表如下
    （1）求频率分布表中x的值；
    （2）如果上学路上所需时间不少于60分钟的学生可申请在学校住宿，请估计学校1000名新生中有多少名学生可以申请住宿；
    （3）现有5名上学路上时间小于40分钟的新生，其中3人上学路上时间不小于20分钟，则从这5人中任选2人，设这2人中上学路上时间小于20分钟人数为X，求X的分布列和数学期望．
    分组频率
    [0，20）0.25
    [20，40）x
    [40，60）0.13
    [60，80）0.06
    [80，100）0.06

    查看答案和解析>>

    同步练习册答案