
| 分组 | 频率 |
| [0,20) | 0.25 |
| [20,40) | x |
| [40,60) | 0.13 |
| [60,80) | 0.06 |
| [80,100) | 0.06 |
分析 (1)由频率分布表的性质能求出x.
(2)先求出新生上学路上所需时间不少于60分钟的频率,由此能求出1000名新生中有多少名学生可以申请住宿.
(3)记5名新生为a、b、c、A、B,(A、B是上学路上时间小于20分钟的新生),利用列举法能求出2人中只有一人上学路上时间小于20分钟的概率.
解答 (1)解:由频率分布表得:0.35+x+0.13+0.06+0.06=1,
∴x=0.50.
(2)解:新生上学路上所需时间不少于60分钟的频率为0.06+0.06=0.12.
1000×0.12=120,
∴1000名新生中有120名学生可以申请住宿.
(3)解:记5名新生为a、b、c、A、B,(A、B是上学路上时间小于20分钟的新生)
从中选2人的所有可能为:ab,ac,aA,aB,bc,bA,bB,cA,cB,AB.共10种.
只有一人上学路上时间都不小于20分钟的有aA,aB,bA,bB,cA,cB,共6种,
∴2人中只有一人上学路上时间小于20分钟的概率p=$\frac{6}{10}$=$\frac{3}{5}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:选择题
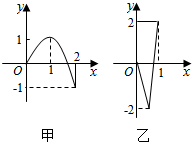 如图,定义在[-2,2]上的偶函数f(x)和定义在[-1,1]上的奇函数g(x)的部分图象分别如图甲、乙,则函数y=f(g(x))的零点个数为( )
如图,定义在[-2,2]上的偶函数f(x)和定义在[-1,1]上的奇函数g(x)的部分图象分别如图甲、乙,则函数y=f(g(x))的零点个数为( )| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2$\sqrt{3}$ | C. | 3 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{6}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com