
| A. | 命题“若a>b,则a2>b2”的否命题是“若a>b,则a2≤b2” | |
| B. | x=2是x2-5x+6=0成立的必要不充分条件 | |
| C. | 命题“若x≠2,则x2-5x+6=0”的逆命题是“若x2-5x+6≠0,则x≠2” | |
| D. | 命题“若α=β,则cosα=cosβ”的逆否命题为真命题 |
分析 A.根据否命题的定义进行判断.
B.根据充分条件和必要条件的定义进行判断.
C.根据逆命题的定义进行判断.
D.根据逆否命题的真假性关系进行判断.
解答 解:A.命题“若a>b,则a2>b2”的否命题是“若a≤b,则a2≤b2”,故A错误,
B.由x2-5x+6=0得x=2或x=3,即x=2是x2-5x+6=0成立的充分不必要条件,故B错误,
C.命题“若x≠2,则x2-5x+6=0”的逆命题是“若x2-5x+6=0,则x≠2”,故C错误,
D.命题“若α=β,则cosα=cosβ”,即原命题成立,则命题的逆否命题也成立,故D正确
故选:D
点评 本题主要考查命题的真假判断,涉及四种命题的关系以及充分条件和必要条件的判断,比较基础.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | ?x∈(0,$\frac{π}{2}$),使得cosx>x | B. | ?x∈(0,$\frac{π}{2}$),使得cosx≥x | ||
| C. | ?x∈(0,$\frac{π}{2}$),使得cosx<x | D. | ?x∈(0,$\frac{π}{2}$),使得cosx<x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 240 | B. | 300 | C. | 360 | D. | 400 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
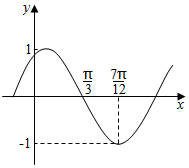 函数f(x)=Asin(ωx+φ)(A>0,|φ|<$\frac{π}{2}$)其中的图象如图所示,为了得到g(x)=cos(2x-$\frac{π}{2}$)的图象,只需将f(x)的图象( )
函数f(x)=Asin(ωx+φ)(A>0,|φ|<$\frac{π}{2}$)其中的图象如图所示,为了得到g(x)=cos(2x-$\frac{π}{2}$)的图象,只需将f(x)的图象( )| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 井号I | 1 | 2 | 3 | 4 | 5 | 6 |
| 坐标(x,y)(km) | (2,30) | (4,40) | (5,60) | (6,50) | (8,70) | (1,y) |
| 钻探深度(km) | 2 | 4 | 5 | 6 | 8 | 10 |
| 出油量(L) | 40 | 70 | 110 | 90 | 160 | 205 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com