
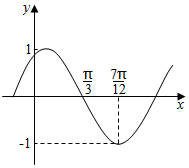
 函数f(x)=Asin(ωx+φ)(A>0,|φ|<$\frac{π}{2}$)其中的图象如图所示,为了得到g(x)=cos(2x-$\frac{π}{2}$)的图象,只需将f(x)的图象( )
函数f(x)=Asin(ωx+φ)(A>0,|φ|<$\frac{π}{2}$)其中的图象如图所示,为了得到g(x)=cos(2x-$\frac{π}{2}$)的图象,只需将f(x)的图象( )| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
分析 根据图象求出φ的值,再由“左加右减”法则判断出函数图象平移的方向和单位长度.
解答 解:∵由函数图象可得:A的值为1,周期T=4×($\frac{7π}{12}$-$\frac{π}{3}$)=π,
∴ω=$\frac{2π}{T}$=$\frac{2π}{π}$=2,
又函数的图象的第二个点是($\frac{π}{3}$,0),
∴2×$\frac{π}{3}$+φ=π,
于是φ=$\frac{π}{3}$,则f(x)=sin(2x+$\frac{π}{3}$)=sin[2(x+$\frac{π}{6}$)],
∵g(x)=cos(2x-$\frac{π}{2}$)=sin2x,
∴为了得到g(x)=cos(2x-$\frac{π}{2}$)的图象,只需将f(x)的图象向右平移$\frac{π}{6}$个单位即可.
故选:D.
点评 本题主要考查了三角函数的函数图象,根据函数图象求解析式,函数y=Asin(ωx+φ)的图象变换规律的应用,注意应用正弦函数图象的关键点进行求解,考查了读图能力和图象变换法则,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若a>b,则a2>b2”的否命题是“若a>b,则a2≤b2” | |
| B. | x=2是x2-5x+6=0成立的必要不充分条件 | |
| C. | 命题“若x≠2,则x2-5x+6=0”的逆命题是“若x2-5x+6≠0,则x≠2” | |
| D. | 命题“若α=β,则cosα=cosβ”的逆否命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | $\frac{π}{3}$ | C. | $\frac{{\sqrt{2}}}{2}π$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com