
分析 可作出图形,取AC中点E,并连接C1E,BE,从而有C1E∥AD,从而得到∠EC1B或其补角便为异面直线AD和BC1所成角,根据条件可以求出△BC1E的三边长度,从而可以得到∠BEC1=90°,然后求sin∠BC1E,这样即可得出异面直线AD和BC1所成角的大小.
解答 解:如图,取AC中点E,连接C1E,BE,则C1E∥AD;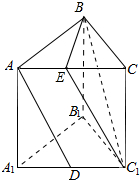
∴∠EC1B或其补角为异面直线AD和BC1所成角;
根据条件得:$BE=\sqrt{2},{C}_{1}E=\sqrt{6},B{C}_{1}=2\sqrt{2}$;
∴$B{E}^{2}+{C}_{1}{E}^{2}=B{{C}_{1}}^{2}$;
∴∠BEC1=90°;
∴$sin∠E{C}_{1}B=\frac{\sqrt{2}}{2\sqrt{2}}=\frac{1}{2}$;
∴∠EC1B=30°;
∴异面直线AD和BC1所成角的大小为30°.
故答案为:30°.
点评 考查异面直线所成角的概念及求法,直角三角形边的关系,正弦函数的定义,以及已知三角函数值求角.


科目:高中数学 来源: 题型:选择题
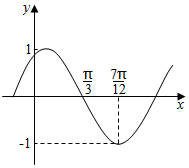 函数f(x)=Asin(ωx+φ)(A>0,|φ|<$\frac{π}{2}$)其中的图象如图所示,为了得到g(x)=cos(2x-$\frac{π}{2}$)的图象,只需将f(x)的图象( )
函数f(x)=Asin(ωx+φ)(A>0,|φ|<$\frac{π}{2}$)其中的图象如图所示,为了得到g(x)=cos(2x-$\frac{π}{2}$)的图象,只需将f(x)的图象( )| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 井号I | 1 | 2 | 3 | 4 | 5 | 6 |
| 坐标(x,y)(km) | (2,30) | (4,40) | (5,60) | (6,50) | (8,70) | (1,y) |
| 钻探深度(km) | 2 | 4 | 5 | 6 | 8 | 10 |
| 出油量(L) | 40 | 70 | 110 | 90 | 160 | 205 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,正四棱台ABCD-A1B1C1D1的上底面边长为1,下底面边长为3,高为1,M为BC的中点,则直线B1M与平面ACC1A1的夹角的正弦值为( )
如图,正四棱台ABCD-A1B1C1D1的上底面边长为1,下底面边长为3,高为1,M为BC的中点,则直线B1M与平面ACC1A1的夹角的正弦值为( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{\sqrt{2}}{6}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com