Question

9．若关于x的不等式$\sqrt{9-{x}^{2}}$≤k（x+1）的解集为区间[a，b]，且b-a≥2，则实数k的取值范围为[$\sqrt{2}$，+∞）．

Answer 1

分析 此不等式属根式不等式，两边平方后再解较繁，可以从数形结合寻求突破．

解答 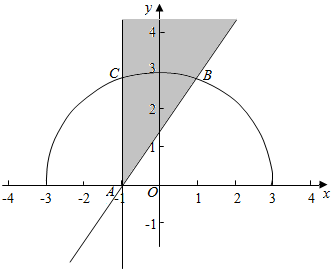解：设y₁=$\sqrt{9-{x}^{2}}$，y₂=k（x+1），
则在同一直角坐标系中作出其图象草图如所示
y₁图象为一圆心在原点，半径为3的圆的上半部分，
y₂图象为过定点A（-1，0）的直线．
据此，原不等式解集可理解为：半圆上圆弧位于直线下方时圆弧上点的横坐标x所对应的集合．
观察图形，结合题意知b=3，或a=-3，
当b=3时，又b-a≥2，所以a≤1，即直线与半圆交点B的横坐标为1，代入y₁=2$\sqrt{2}$，
则k（1+1）=2$\sqrt{2}$，
解得k=$\sqrt{2}$，
当a=-3时，又b-a≥2，所以b≥-1，即直线与半圆交点C的横坐标为-1，代入y₁=2$\sqrt{2}$，
此时k的不存在，
终上所述k的取值范围k≥$\sqrt{2}$，
故答案为：[$\sqrt{2}$，+∞）．

点评 数形结合是研究不等式解的有效方法，数形结合使用的前提是：掌握形与数的对应关系．基本思路是：①构造函数f（x）（或f（x）与g（x）），②作出f（x） （或f（x）与g（x））的图象，③找出满足题意的曲线（部分），曲线上点的横坐标为题目的解，并研究解的特性来确定解题的切入点．