
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
分析 将方程的解的个数转化为两个函数的交点问题,通过图象即可解答.
解答 解:函数y=|log2x|-${(\frac{1}{2})}^{|x|}$的零点个数,是方程|log2x|-${(\frac{1}{2})}^{|x|}$=0的实数根的个数,
即|log2x|=${(\frac{1}{2})}^{|x|}$,
令f(x)=|log2x|,g(x)=${(\frac{1}{2})}^{|x|}$,
画出函数的图象,如图所示:
由图象得:f(x)与g(x)有2个交点,
∴方程|log2x|-${(\frac{1}{2})}^{|x|}$=0解的个数为2个,
故选:C.
点评 本题考查了函数零点的应用问题,也考查了转化思想,数形结合思想的应用问题,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\frac{{\sqrt{x}}}{2}$ | B. | y=(x-1)2 | C. | y=2-x | D. | y=log0.5x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针指向位置P(x,y),若初如位置为${P_0}(\frac{{\sqrt{3}}}{2},\frac{1}{2})$,秒针从P0(注:此时t=0)开始沿顺时针方向走动,则点P的纵坐标y与时间t的函数关系为( )
为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针指向位置P(x,y),若初如位置为${P_0}(\frac{{\sqrt{3}}}{2},\frac{1}{2})$,秒针从P0(注:此时t=0)开始沿顺时针方向走动,则点P的纵坐标y与时间t的函数关系为( )| A. | $y=sin(\frac{π}{30}t+\frac{π}{6})$ | B. | $y=sin(-\frac{π}{60}t-\frac{π}{6})$ | C. | $y=sin(-\frac{π}{30}t+\frac{π}{6})$ | D. | $y=sin(-\frac{π}{30}t-\frac{π}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
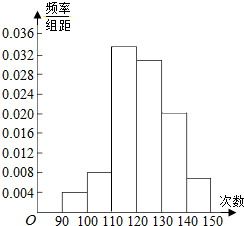 为了了解高一学生的体能情况,某校抽取部分学生进行一部分跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12,若次数在110以上(含110次)为达标,试估计该学校全体高一学生单调达标率是0.88.
为了了解高一学生的体能情况,某校抽取部分学生进行一部分跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12,若次数在110以上(含110次)为达标,试估计该学校全体高一学生单调达标率是0.88.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -7 | B. | 7 | C. | -$\frac{3}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com