练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．已知角θ的终边经过点P（-x，-6），且cosθ=-$\frac{3}{5}$，则x=（　　）
    A．$\frac{9}{2}$B．-$\frac{9}{2}$C．$\frac{2}{9}$D．-$\frac{2}{9}$

    分析 根据题意，由点P的坐标可得r=|OP|的值，由三角函数余弦的定义可得cosθ=$\frac{-x}{\sqrt{{x}^{2}+36}}$=-$\frac{3}{5}$，解可得x的值，即可得答案．

    解答 解：根据题意，角θ的终边经过点P（-x，-6），
    则r=|OP|=$\sqrt{（-x）^{2}+{6}^{2}}$=$\sqrt{{x}^{2}+36}$，
    则cosθ=$\frac{-x}{\sqrt{{x}^{2}+36}}$=-$\frac{3}{5}$，
    解可得x=$\frac{9}{2}$；
    故选：A．

    点评 本题考查任意角三角函数的定义，关键是牢记任意角三角函数的定义并熟练运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    14．已知x，y满足：$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1，那么
    （1）求函数x2+xy+y2的最值；
    （2）求函数3x+4y的最值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知定义在R上的函数f（x）满足f（x）+$\frac{1}{2}cos2x$在（0，+∞）上是减函数，且?x∈R，有f（-x）+f（x）=2sin2x，则以下大小关系一定正确的是（　　）
    A．f（$\frac{5π}{6}$）＜f（$\frac{4π}{3}$）B．f（$\frac{π}{4}$）＜f（π）C．f（-$\frac{5π}{6}$）＜f（-$\frac{4π}{3}$）D．f（-$\frac{π}{4}$）＜f（-π）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知Sn为公比不为1的等比数列{an}的前n项和，$\frac{{S}_{3}}{{a}_{3}}$=3，则$\frac{{S}_{5}}{{a}_{6}}$等于62．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．一辆汽车在司机猛踩刹车后5s内停下．在这一刹车过程中，下面各速度值被记录了下来：
     刹车踩下后的时间/s 0 12  3 4 5
     速度/（m•s-1） 2718  127 3 0
    求刹车踩下后汽车滑过的距离的不足近似值（每个ξi均取为小区间的右端点）与过剩近似值（每个ξi均取为小区间的左端点）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．若关于x的不等式$\sqrt{9-{x}^{2}}$≤k（x+1）的解集为区间[a，b]，且b-a≥2，则实数k的取值范围为[$\sqrt{2}$，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知数列{an}满足a1=1，an=an-1+n，求此数列的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．（x-y）（x+y）5展开式中，x4y2的系数为（　　）
    A．5B．-5C．10D．-10

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

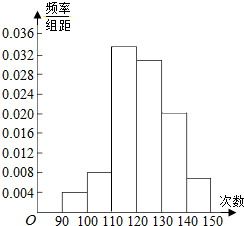    10．为了了解高一学生的体能情况，某校抽取部分学生进行一部分跳绳次数测试，将所得数据整理后，画出频率分布直方图（如图所示），图中从左到右各小长方形面积之比为2：4：17：15：9：3，第二小组频数为12，若次数在110以上（含110次）为达标，试估计该学校全体高一学生单调达标率是0.88．

    查看答案和解析>>

    同步练习册答案