

(1)求证:![]() ;
;
(2)求![]() 的值.
的值.
(1)证明:∵a2=![]() m2,b2=
m2,b2=![]() m2,
m2,
∴c2=a2-b2=m2.
∴F(m,0).
∵直线l过焦点F(m,0)且与向量a=(1,1)?平行,
∴直线l的方程为y=x-m.
将其代入椭圆C的方程,并整理可得8x2-10mx-![]() m2=0.①
m2=0.①
设A(xA,yA),B(xB,yB),M(xM,yM),N(xN,yN).
∵M是线段AB的中点,在方程①中由韦达定理,可得xM=![]() =
=![]() m,yM=xM-m=-
m,yM=xM-m=-![]() m,
m,
∴M(![]() m,-
m,-![]() m).
m).
设N′为OM延长线上的点,且M为ON′的中点,则N′(![]() m,-
m,-![]() m),且四边形OAN′B为平行四边形.
m),且四边形OAN′B为平行四边形.
将N′的坐标代入椭圆C方程的左端并化简得![]() ·(
·(![]() m)2+
m)2+![]() ·(-
·(-![]() m)2=
m)2=![]() m2,
m2,
∴N′点在椭圆C上,N′与N点重合.
∴四边形OANB为平行四边形,于是![]() +
+![]() =
=![]() .
.
(2)解:∵![]() ·
·![]() =xAxB+yAyB,
=xAxB+yAyB,
在方程①中由韦达定理,得xAxB=-![]() m2,
m2,
∴yAyB=(xA-m)(xB-m)=xAxB-m(xA+xB)+m2
=-![]() m2-
m2-![]() m2+m2
m2+m2
=-![]() m2.1
m2.1
∴![]() ·
·![]() =-
=-![]() m2-
m2-![]() m2=-
m2=-![]() m2.
m2.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 4 |
| x2 |
| 16 |
| y2 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
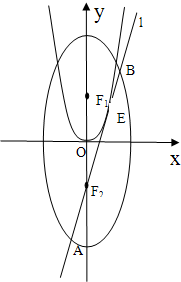 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| b2 |
| y2 |
| a2 |
| F2B |
| AF2 |
| ET |
| EF1 |
| EF2 |
| 1 |
| 2 |
| ET |
| OT |
| 5 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| F1A |
| F2A |
| π |
| 3 |
| 2π |
| 3 |
4
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
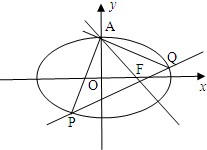 (2012•梅州一模)如图,已知椭圆C:
(2012•梅州一模)如图,已知椭圆C:| x2 |
| a2 |
| AP |
| AQ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com