
【题目】已知函数![]() .
.
(1)若函数![]() 在定义域上是单调增函数,求
在定义域上是单调增函数,求![]() 的最小值;
的最小值;
(2)若方程![]() 在区间
在区间![]() 上有两个不同的实根,求
上有两个不同的实根,求![]() 的取值范围.
的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.圆锥的底面是圆面,侧面是曲面
B.用一张扇形的纸片可以卷成一个圆锥
C.一个物体上、下两个面是相等的圆面,那么它一定是一个圆柱
D.圆台的任意两条母线的延长线可能相交也可能不相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,椭圆
,椭圆![]() 过点
过点 ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,且
,且![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 的上顶点,过点
的上顶点,过点![]() 分别作直线
分别作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为![]() ,且
,且![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】脱贫是政府关注民生的重要任务,了解居民的实际收入状况就显得尤为重要.现从某地区随机抽取![]() 个农户,考察每个农户的年收入与年积蓄的情况进行分析,设第
个农户,考察每个农户的年收入与年积蓄的情况进行分析,设第![]() 个农户的年收入
个农户的年收入![]() (万元),年积蓄
(万元),年积蓄![]() (万元),经过数据处理得
(万元),经过数据处理得![]()
(Ⅰ)已知家庭的年结余![]() 对年收入
对年收入![]() 具有线性相关关系,求线性回归方程;
具有线性相关关系,求线性回归方程;
(Ⅱ)若该地区的农户年积蓄在![]() 万以上,即称该农户已达小康生活,请预测农户达到小康生活的最低年收入应为多少万元?
万以上,即称该农户已达小康生活,请预测农户达到小康生活的最低年收入应为多少万元?
附:在![]() 中,
中, 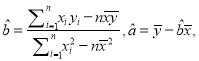 其中
其中![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】脱贫是政府关注民生的重要任务,了解居民的实际收入状况就显得尤为重要.现从某地区随机抽取![]() 个农户,考察每个农户的年收入与年积蓄的情况进行分析,设第
个农户,考察每个农户的年收入与年积蓄的情况进行分析,设第![]() 个农户的年收入
个农户的年收入![]() (万元),年积蓄
(万元),年积蓄![]() (万元),经过数据处理得
(万元),经过数据处理得![]()
(Ⅰ)已知家庭的年结余![]() 对年收入
对年收入![]() 具有线性相关关系,求线性回归方程;
具有线性相关关系,求线性回归方程;
(Ⅱ)若该地区的农户年积蓄在![]() 万以上,即称该农户已达小康生活,请预测农户达到小康生活的最低年收入应为多少万元?
万以上,即称该农户已达小康生活,请预测农户达到小康生活的最低年收入应为多少万元?
附:在![]() 中,
中,  其中
其中![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的损坏,可见部分如下:

试着根据表中的信息解答下列问题:
(Ⅰ)求全班的学生人数及分数在[70,80)之间的频数;
(Ⅱ)为快速了解学生的答题情况,老师按分层抽样的方法从位于[70,80)和[80,90)分数段的试卷中抽取7份进行分析,再从中任选2人进行交流,求交流的学生中,成绩位于[70,80)分数的人恰有一人被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海州市英才中学某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分別到气象局与某医院抄录了![]() 至
至![]() 月份每月
月份每月![]() 号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料(表):
号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料(表):
日期 |
|
|
|
|
|
|
昼夜温差 |
|
|
|
|
|
|
就诊人数 |
|
|
|
|
|
|
该兴趣小组确定的研究方案是:先从这六组数据中选取![]() 组,用剩下的
组,用剩下的![]() 组数据求线性回归方程,再用被选取的
组数据求线性回归方程,再用被选取的![]() 组数据进行检验.
组数据进行检验.
(1)求选取的![]() 组数据恰好是相邻两个月的概率;
组数据恰好是相邻两个月的概率;
(2)若选取的是![]() 月与6月的两组数据,请根据
月与6月的两组数据,请根据![]() 至
至![]() 月份的数据,求出
月份的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过![]() 人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想.
人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想.
其中回归系数公式, ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是
,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于两点A,B,且![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com