练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】脱贫是政府关注民生的重要任务，了解居民的实际收入状况就显得尤为重要.现从某地区随机抽取个农户，考察每个农户的年收入与年积蓄的情况进行分析，设第个农户的年收入（万元），年积蓄（万元），经过数据处理得

    （Ⅰ）已知家庭的年结余对年收入具有线性相关关系，求线性回归方程；

    （Ⅱ）若该地区的农户年积蓄在万以上，即称该农户已达小康生活，请预测农户达到小康生活的最低年收入应为多少万元？

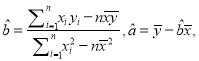    附：在 中， 其中为样本平均值.

    【答案】（Ⅰ） ;（Ⅱ）万元.

    【解析】试题分析：(Ⅰ)利用题中所给数据和最小二乘法求出相关系数，进而求出线性回归方程；（Ⅱ）利用线性回归方程进行预测.

    试题解析：（Ⅰ）由题意知所以线性回归方程为

    （Ⅱ）令 得

    由此可预测该农户的年收入最低为万元.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】投掷一个质地均匀的、每个面上标有一个数字的正方体玩具，它的六个面中，有两个面标的数字是0，两个面标的数字是2，两个面标的数字是4，将此玩具连续抛掷两次，以两次朝上一面的数字分别作为点P的横坐标和纵坐标.

    （1）求点P落在区域C：x2＋y2≤10内的概率；

    （2）若以落在区域C上的所有点为顶点作面积最大的多边形区域M，在区域C上随机撒一粒豆子，求豆子落在区域M上的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一条直线和三角形的两边同时垂直，则这条直线和三角形的第三边的位置关系是（ ）

    A.平行B.垂直C.相交不垂直D.不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列调查方式中合适的是（ ）

    A.要了解一批节能灯的使用寿命，采用普查方式

    B.调查你所在班级同学的身高，采用抽样调查方式

    C.调查沱江某段水域的水质情况，采用抽样调查方式

    D.调查全市中学生每天的就寝时间，采用普查方式

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，已知圆C：（x﹣2）2+（y+1）2=5，过点P（5，0）且斜率为k的直线与圆C相交于不同的两点A，B．

    （I）求k的取值范围；

    （Ⅱ）若弦长|AB|=4，求直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，且．

    （1）若函数在区间上是减函数，求实数的取值范围；

    （2）设函数，当时， 恒成立，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）若函数在定义域上是单调增函数，求的最小值；

    （2）若方程在区间上有两个不同的实根，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的顶点到左焦点的距离为，离心率.

    （1）求椭圆的方程；

    （2）若点为椭圆的右頂点,过点作互相垂直的两条射线,与椭圆分別交于不同的两点不与左、右顶点重合) ，试判断直线是否过定点，若过定点，求出该定点的坐标；若不过定点，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为调查甲、乙两校高三年级学生某次联考数学成绩情况，用简单随机抽样，从这两校中各抽取30名高三年级学生，以他们的数学成绩（百分制）作为样本，样本数据的茎叶图如图．

    （1）若甲校高三年级每位学生被抽取的概率为0.05，求甲校高三年级学生总人数，并估计甲校高三年级这次联考数学成绩的及格率（60分及60分以上为及格）；

    （2）设甲、乙两校高三年级学生这次联考数学平均成绩分别为1，2，估计1－2的值．

    查看答案和解析>>

    同步练习册答案