
| 日均阅读小说时间(分钟) | (0,30] | (30,60] | (60,90] | (90,120] | (120,150] | (150,+∞) |
| 人数 | 15 | 21 | 24 | 28 | 8 | 4 |
| 非小说迷 | 小说迷 | 合计 | |
| 男 | 15 | 48 | |
| 女 | |||
| 合计 |
| P(K2≥k0) | 0.50 | 0.25 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 1.323 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)根据已知条件完成2×2列联表,根据此资料,求出K2≈2.944>2.706,从而有90%的把握认为“小说迷”与性别有关.
(2)由数据可知任抽一人,抽到“小说迷”的频率为0.4,由题意X~B(3,$\frac{2}{5}$),由此能求出X的分布列和EX.
解答 解:(1)根据已知条件2×2列联表如下:
| 非小说迷 | 小说迷 | 合计 | |
| 男 | 33 | 15 | 48 |
| 女 | 27 | 25 | 52 |
| 合计 | 60 | 40 | 100 |
| X | 0 | 1 | 2 | 3 |
| P | $\frac{27}{125}$ | $\frac{54}{125}$ | $\frac{36}{125}$ | $\frac{8}{125}$ |
点评 本题考查独立检验的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{4\sqrt{6}-7}{18}$ | B. | $\frac{7-4\sqrt{6}}{18}$ | C. | $\frac{\sqrt{3}+\sqrt{2}}{6}$ | D. | $\frac{\sqrt{3}-\sqrt{2}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
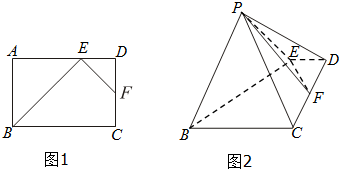 如图1,在矩形ABCD中,点E为边AD上靠近D的三等分点,点F为边CD的中点,AB=AE=4,现将△ABE沿BE边折至△PBE位置,且平面PBE⊥平面BCDE.
如图1,在矩形ABCD中,点E为边AD上靠近D的三等分点,点F为边CD的中点,AB=AE=4,现将△ABE沿BE边折至△PBE位置,且平面PBE⊥平面BCDE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -$\frac{3}{4}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com