
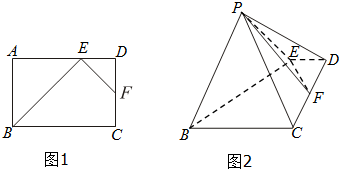
 如图1,在矩形ABCD中,点E为边AD上靠近D的三等分点,点F为边CD的中点,AB=AE=4,现将△ABE沿BE边折至△PBE位置,且平面PBE⊥平面BCDE.
如图1,在矩形ABCD中,点E为边AD上靠近D的三等分点,点F为边CD的中点,AB=AE=4,现将△ABE沿BE边折至△PBE位置,且平面PBE⊥平面BCDE.分析 (1)利用折叠前的图形可判断BE⊥EF,由面面垂直的性质可得EF⊥平面PBE,再由线面垂直得面面垂直;
(2)过P做PO⊥BE,由面面垂直的性质及线面垂直的判定得到PO⊥平面BCDE,即PO为四棱锥P-BCFE的高.把S四边形BCFE转化为S矩形ABCD-S△ABE-S△DEF,求值后代入棱锥的体积公式得答案.
解答 (1)证明:∵点E为边AD上靠近D的三等分点,点F为边CD的中点,AB=AE=4,
∴$AB=AE=\frac{2}{3}AD=4$,
∴DE=$\frac{1}{3}$AD=$\frac{1}{2}$AB=2,
∵F为CD边的中点,
∴DE=DF,又DE⊥DF,
∴∠DEF=45°,
同理∠AEB=45°,
∴∠BEF=45°,即EF⊥BE,
又平面ABE⊥平面BCDE,平面ABE∩平面BCDE=BE,
∴EF⊥平面PBE,
EF?平面PEF,
∴平面PBE⊥平面PEF;如图,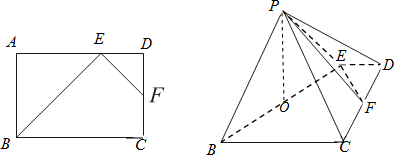 在Rt△DEF中,∵ED=DF,∴∠DEF=45°.
在Rt△DEF中,∵ED=DF,∴∠DEF=45°.
在Rt△ABE中,∵AE=AB,∴∠AEB=45°,
∴∠BEF=90°,则EF⊥BE.
∵平面PBE⊥平面BCDE,且平面PBE∩平面BCDE=BE,
∴EF⊥平面PBE,
∵EF?平面PEF,∴平面PBE⊥平面PEF;
(2)解:过P做PO⊥BE,
∵PO?平面PBE,平面PBE⊥平面BCDE且平面PBE∩平面BCDE=BE,
∴PO⊥平面BCDE,
四棱锥P-BCFE的高h=PO=$2\sqrt{2}$.
S四边形BCFE=S矩形ABCD-S△ABE$-{S}_{△DEF}=6×4-\frac{1}{2}×4×4-\frac{1}{2}×2×2=14$,
则${V}_{P-BCFE}=\frac{1}{3}{S}_{四边形BCFE}•h$=$\frac{1}{3}×14×2\sqrt{2}=\frac{28\sqrt{2}}{3}$.
点评 本题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $-\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知ABCD是矩形,AD=2AB,E,F分别是线段AB,BC的中点,PA⊥平面ABCD.
已知ABCD是矩形,AD=2AB,E,F分别是线段AB,BC的中点,PA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日均阅读小说时间(分钟) | (0,30] | (30,60] | (60,90] | (90,120] | (120,150] | (150,+∞) |
| 人数 | 15 | 21 | 24 | 28 | 8 | 4 |
| 非小说迷 | 小说迷 | 合计 | |
| 男 | 15 | 48 | |
| 女 | |||
| 合计 |
| P(K2≥k0) | 0.50 | 0.25 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 1.323 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称为入肺颗粒物),为了探究车流量与PM2.5的浓度失分相关,现采集某城市周一至周五时间段车流量与PM2.5的数据如表”
PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称为入肺颗粒物),为了探究车流量与PM2.5的浓度失分相关,现采集某城市周一至周五时间段车流量与PM2.5的数据如表”| 时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 车流量x(万辆) | 50 | 51 | 54 | 57 | 58 |
| PM2.5的浓度y(微克/立方米) | 69 | 70 | 74 | 78 | 79 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com