
分析 (1)抛物线的顶点在原点,准线方程为x=1,可得抛物线的方程;依题意,设直线AB的方程为x=my-2,与抛物线方程联立消x得关于y的一元二次方程,根据韦达定理即可求得y1y2;
(2)设M(x3,y3),N(x4,y4),设直线AM的方程为x=ny-1,将其代入y2=-4x,消去x,得到关于y的一元二次方程,从而得y1y3=-4,同理可得 y2y4=-4,根据斜率公式可把$\frac{{k}_{1}}{{k}_{2}}$表示成关于y1与y2的表达式,再借助(1)的结果即可证明.
解答 (1)解:抛物线的顶点在原点,准线方程为x=1,∴抛物线的方程为y2=-4x,
设PQ的方程为x=my-2,代入y2=-4x,可得y2+4my-8=0
∴y1y2=-8;
(2)证明:设M(x3,y3),N(x4,y4).
则$\frac{{k}_{1}}{{k}_{2}}$=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}•\frac{{x}_{3}-{x}_{4}}{{y}_{3}-{y}_{4}}$=$\frac{{y}_{3}+{y}_{4}}{{y}_{1}+{y}_{2}}$
设直线PM的方程为x=ny-1(n≠0),将其代入y2=-4x,消去x,
整理得 y2+4ny-4=0
∴y1y3=-4.
同理可得 y2y4=-4.
故$\frac{{k}_{1}}{{k}_{2}}$=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}•\frac{{x}_{3}-{x}_{4}}{{y}_{3}-{y}_{4}}$=$\frac{{y}_{3}+{y}_{4}}{{y}_{1}+{y}_{2}}$=-$\frac{4}{{y}_{1}{y}_{2}}$.
由(1)知,y1y2=-8,
∴$\frac{{k}_{1}}{{k}_{2}}$=$\frac{1}{2}$为定值.
点评 本题考查直线与圆锥曲线的位置关系及抛物线的简单性质,考查学生综合运用知识分析问题解决问题的能力,难度较大.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(文)试卷(解析版) 题型:选择题
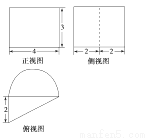
已知一几何体的三视图如图所示,俯视图是由一个直角三角形与一个半圆组成,则该几何体的体积为( )
A. 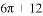 B.
B. 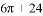 C.
C.  D.
D. 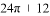
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(理)试卷(解析版) 题型:选择题
在斜△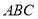 中,角
中,角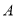 ,
,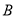 ,
,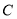 所对的边长分别为
所对的边长分别为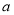 ,
,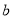 ,
,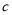 ,
,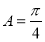 ,
,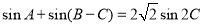 ,且△
,且△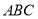 的面积为1,则
的面积为1,则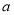 的值为( )
的值为( )
A. B.
B.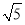 C.
C.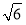 D.
D.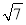
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(理)试卷(解析版) 题型:选择题
下列结论判断正确的是( )
A.棱长为1的正方体的内切球的表面积为
B.三条平行直线最多确定三个平面
C.正方体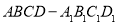 中,
中, 与
与 异面
异面
D.若平面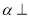 平面
平面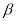 ,平面
,平面 平面
平面 ,则平面
,则平面 平面
平面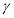
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{3π}{8}$ | D. | $\frac{π}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
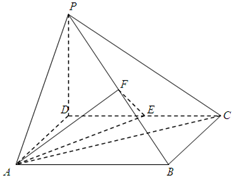 如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD=2,E、F分别为CD、PB的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD=2,E、F分别为CD、PB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com