
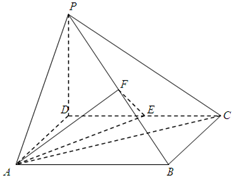
 如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD=2,E、F分别为CD、PB的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD=2,E、F分别为CD、PB的中点.分析 方法一;(1)取PA中点G,连结DG、FG,要证明EF∥平面PAD,我们可以证明EF与平面PAD中的直线AD平行,根据E、F分别是PB、PC的中点,利用中位线定理结合线面平行的判定定理,即可得到答案.
(2)根据线面垂直的和面面垂直的判断定理即可证明.
方法二:(1)求出直线EF所在的向量,得到$\overrightarrow{EF}$=$\frac{1}{2}$($\overrightarrow{DP}$+$\overrightarrow{DA}$)=$\frac{1}{2}$$\overrightarrow{DP}$+$\frac{1}{2}$$\overrightarrow{DA}$,即可证明EF∥平面PAD.
(2)再求出平面内两条相交直线所在的向量,然后利用向量的数量积为0,根据线面垂直的判定定理得到线面垂直,即可证明平面AEF⊥平面PAB
(3)求出平面的法向量以及直线所在的向量,再利用向量的有关运算求出两个向量的夹角,进而转化为线面角,即可解决问题.
解答  证明:方法一:(1)取PA中点G,连结DG、FG.
证明:方法一:(1)取PA中点G,连结DG、FG.
∵F是PB的中点,
∴GF∥AB且GF=$\frac{1}{2}$AB,
又底面ABCD为矩形,E是DC中点,
∴DE∥AB且DE=$\frac{1}{2}$AB
∴GF∥DE且GF=DE,
∴四边形DEFG为平行四边形
∴EF∥DG
∵DG?平面PAD,EF?平面PAD,
∴EF∥平面PAD.
(2)∵PD⊥底面ABCD,AB?面ABCD
∴PD⊥AB
又底面ABCD为矩形
∴AD⊥AB
又PD∩AD=D
∴AB⊥平面PAD
∵DG?平面PAD
∴AB⊥DG
∵AD=PD,G为AP中点
∴DG⊥AP
又AB∩AP=A,
∴DG⊥平面PAB
又由(1)知EF∥DG
∴EF⊥平面PAB,
又EF?面AEF∴平面AEF⊥平面PAB.
证法二:(1)以D为坐标原点,DA、DC、DP所在直线分别为x轴、y轴、z轴,建立如图所示空间直角坐标系.设AB=a.
∵AD=PD=2,
∴A(2,0,0),B(2,a,0),C(0,a,0),P(0,0,2),
∵E、F分别为CD,PB的中点
∴E(0,$\frac{a}{2}$,0),F(1,$\frac{a}{2}$,0).
∴$\overrightarrow{EF}=(1,0,1)$,
∵$\overrightarrow{DP}$+$\overrightarrow{DA}$=(0,0,2)+(2,0,0)=(2,0,2),
∴$\overrightarrow{EF}$=$\frac{1}{2}$($\overrightarrow{DP}$+$\overrightarrow{DA}$)=$\frac{1}{2}$$\overrightarrow{DP}$+$\frac{1}{2}$$\overrightarrow{DA}$,
故$\overrightarrow{EF}$、$\overrightarrow{DP}$、$\overrightarrow{DA}$共面,
又EF?平面PAD
∴EF∥平面PAD.
(2)由(1)知$\overrightarrow{EF}=(1,0,1)$,$\overrightarrow{AB}=(0,a,0)$,$\overrightarrow{AP}=(-2,0,2)$.
∴$\overrightarrow{EF}•\overrightarrow{AB}$=0,$\overrightarrow{EF}$•$\overrightarrow{AP}$=-2+0+2=0,
∴$\overrightarrow{EF}$⊥$\overrightarrow{AB}$,$\overrightarrow{EF}$⊥$\overrightarrow{AP}$,
又AB∩AP=A,
∴EF⊥平面PAB,
又EF?平面AEF,
∴平面AEF⊥平面PAB,
(3)AB=2$\sqrt{2}$由(1)知,
∴$\overrightarrow{AE}$=(-2,$\sqrt{2}$,0),$\overrightarrow{EF}$=(1,0,1)
设平面AEF的法向量$\overrightarrow n=(x,y,z)$,
则$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{AE}=0\\ \overrightarrow n•\overrightarrow{EF}=0\end{array}\right.即\left\{\begin{array}{l}-2x+\sqrt{2}y=0\\ x+z=0\end{array}\right.$,
令x=1,则y=$\sqrt{2}$,z=-1,
∴$\overrightarrow{n}$=(1,$\sqrt{2}$,-1),
又$\overrightarrow{AC}$=(-2,2$\sqrt{2}$,0),
∴cos<$\overrightarrow{AC}$,$\overrightarrow{n}$>=$\frac{-2+4+0}{2\sqrt{12}}$=$\frac{\sqrt{3}}{6}$,
∴sinθ=|cos<$\overrightarrow{AC}$,$\overrightarrow{n}$>|=$\frac{\sqrt{3}}{6}$.
点评 本题考查了本题考查的知识点是直线与平面平行的判定,面面垂直,直线与平面所成的角,解决此类问题的关键是熟练掌握几何体的结构特征,进而得到空间中点、线、面的位置关系,利于建立空间之间坐标系,利用向量的有关知识解决空间角与空间距离以及线面的位置关系等问题,属于中档题.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高一上国庆作业二数学试卷(解析版) 题型:解答题
已知函数 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时有
时有 .
.
①求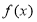 的解析式;
的解析式;
②求 的值域;
的值域;
③若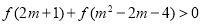 ,求
,求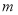 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
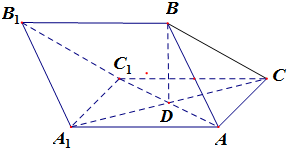 在三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,BC=$\sqrt{6}$,AC1与A1C相交于点D.
在三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,BC=$\sqrt{6}$,AC1与A1C相交于点D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com