
分析 (Ⅰ)联立C1与C2的极坐标方程$\left\{\begin{array}{l}ρ=4sinθ\\ ρ=4cos(θ+\frac{π}{6})\end{array}\right.$,求解即可得到结果.
(Ⅱ)由(Ⅰ)得点B的直角坐标为$B(\sqrt{3},1)$,将圆C1的极坐标方程化为直角坐标方程,求出圆心C1(0,2),设点P对应的参数为λ,可得$P(\sqrt{3}-\frac{{\sqrt{3}}}{2}λ,1+\frac{1}{2}λ)$,利用$\overrightarrow{BP}=m\overrightarrow{B{C_1}}$,求解即可.
解答 解:(Ⅰ)联立C1与C2的极坐标方程$\left\{\begin{array}{l}ρ=4sinθ\\ ρ=4cos(θ+\frac{π}{6})\end{array}\right.$,得$4sinθ=4cos(θ+\frac{π}{6})$,
当ρ=0时,得交点A极坐标为A(0,0),-------------------------------------(2分)
当ρ≠0时,化简得$tanθ=\frac{{\sqrt{3}}}{3}$,从而$θ=\frac{π}{6}$,ρ=2或$θ=\frac{7π}{6}$,ρ=-2(舍去),
∴点B的极坐标是$B(2,\frac{π}{6})$.----------------------------------------------(5分)
(Ⅱ)由(Ⅰ)得点B的直角坐标为$B(\sqrt{3},1)$,
将圆C1的极坐标方程化为直角坐标方程得x2+(y-2)2=4,
从而C1的直角坐标为C1(0,2),
设点P对应的参数为λ,即$P(\sqrt{3}-\frac{{\sqrt{3}}}{2}λ,1+\frac{1}{2}λ)$,----------------------------(7分)
则$\overrightarrow{BP}=(-\frac{{\sqrt{3}}}{2}λ,\frac{1}{2}λ)$,$\overrightarrow{B{C_1}}=(-\sqrt{3},1)$,由$\overrightarrow{BP}=m\overrightarrow{B{C_1}}$,得$\left\{\begin{array}{l}-\frac{{\sqrt{3}}}{2}λ=-m\sqrt{3}\\ \frac{1}{2}λ=m\end{array}\right.$,
∴m:λ=1:2-----------------------------------------------------------(10分)
点评 本题考查直线的参数方程以及圆的极坐标方程的应用,与普通方程的互化,考查计算能力.


科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(文)试卷(解析版) 题型:解答题
执行如图所示的程序框图.
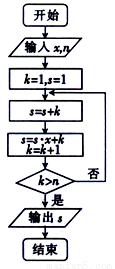
(1)若输入的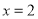 ,
,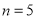 ,求输出的
,求输出的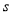 的值;
的值;
(2)若输入的 ,输出的
,输出的 ,求输入的
,求输入的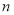 (
(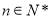 )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.852 | B. | 0.8192 | C. | 0.8 | D. | 0.75 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高一上国庆作业二数学试卷(解析版) 题型:解答题
已知函数 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时有
时有 .
.
①求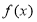 的解析式;
的解析式;
②求 的值域;
的值域;
③若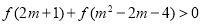 ,求
,求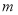 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com