
分析 (1)由题意,列出关于a,b,c的方程组,解得即可,则椭圆方程可求;
(2)设直线l:x=my+n点M(x1,y1),N(x2,y2),与椭圆方程联立,利用根与系数的关系及$\overrightarrow{AM}•\overrightarrow{AN}$=0,求出x=m(y+$\frac{3}{14}$)+$\frac{1}{7}$,即可得到直线过定点.
解答 解:(1)设椭圆的方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),则由已知可得:$\left\{\begin{array}{l}{\frac{1}{{a}^{2}}+\frac{\frac{9}{4}}{{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\frac{\frac{3}{2}}{1+c}=\frac{3}{4}}\end{array}\right.$,解得a=2,b=$\sqrt{3}$,c=1,
则椭圆的方程为:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,
(2)设直线l:x=my+n点M(x1,y1),N(x2,y2).直线l与椭圆C的方程联立,消去x得,(4+3m2)y2+8mny+3m2-12=0,
∴y1+y2=-$\frac{6mn}{3{m}^{2}+4}$,y1y2=$\frac{3{n}^{2}-12}{3{m}^{2}+4}$,①
同理可得:x1+x2=$\frac{8n}{3{m}^{2}+4}$,x1x2=$\frac{4{n}^{2}-12{m}^{2}}{3{m}^{2}+4}$,②,
又由∠MAN=90°,则$\overrightarrow{AM}•\overrightarrow{AN}$=0,
∴(x1-1,y1-$\frac{3}{2}$)•(x2-1,y2-$\frac{3}{2}$)=x1x2-(x1+x2)+y1y2-$\frac{3}{2}$(y1+y2)+$\frac{13}{4}$=0③
将①②代入③整理得:3($\frac{3}{2}$m+n)2+4(n-1)2-9m2-3=0,
也就是3($\frac{3}{2}$m+n-1)($\frac{3}{2}$m+n+1)+4(n-1-$\frac{3}{2}$m)(n-1+$\frac{3}{2}$m)=0,
由于点A不在直线l上,则$\frac{3}{2}$m+n-1≠0则,
3($\frac{3}{2}$m+n+1)+4(n-1-$\frac{3}{2}$m)=0,整理n=$\frac{2+3m}{14}$,
则x=my+n=my+$\frac{2+3m}{14}$=m(y+$\frac{3}{14}$)+$\frac{1}{7}$,
所以直线l过定点($\frac{1}{7}$,-$\frac{3}{14}$)
点评 本题考查椭圆标准方程的求法,考查了直线与圆锥曲线位置关系的应用,训练了存在性问题的求解方法,考查了数形结合的思想、推理能力和计算能力,属难题.


科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(理)试卷(解析版) 题型:选择题
在斜△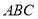 中,角
中,角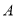 ,
,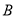 ,
,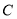 所对的边长分别为
所对的边长分别为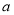 ,
,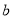 ,
,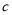 ,
,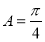 ,
,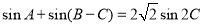 ,且△
,且△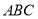 的面积为1,则
的面积为1,则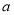 的值为( )
的值为( )
A. B.
B.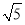 C.
C.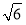 D.
D.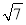
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{3π}{8}$ | D. | $\frac{π}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
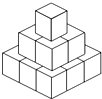 把14个棱长为1的正方体,在地面上堆叠成如图所示的几何体,然后将露出的表面部分染成红色.那么红色部分的面积为( )
把14个棱长为1的正方体,在地面上堆叠成如图所示的几何体,然后将露出的表面部分染成红色.那么红色部分的面积为( )| A. | .21 | B. | .24 | C. | .33 | D. | .37 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com