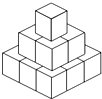
把14个棱长为1的正方体.在地面上堆叠成如图所示的几何体.然后将露出的表面部分染成红色．那么红色部分的面积为( )A．.21B．.24C．.33D．.37 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

3．

把14个棱长为1的正方体，在地面上堆叠成如图所示的几何体，然后将露出的表面部分染成红色．那么红色部分的面积为（　　）

A．

.21

B．

.24

C．

.33

D．

.37

分析此题可根据表面积的计算分层计算得出红色部分的面积再相加．

解答解：根据题意得：
第一层露出的表面积为：1×1×6-1×1=5，
第二层露出的表面积为：1×1×6×4-1×1×13=11，
第三层露出的表面积为：1×1×6×9-1×1×37=17，
所以红色部分的面积为：5+11+17=33，
故选：C．

点评此题考查的知识点是几何体的表面积，关键是在计算表面积时减去不露的或重叠的面积．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源：2017届安徽合肥一中高三上学期月考一数学（理）试卷（解析版） 题型：选择题

已知函数（且）的图象恒过定点，则点的坐标是（）

A． B． C． D．

查看答案和解析>>

科目：高中数学 来源：2016-2017学年河北正定中学高二上月考一数学（理）试卷（解析版） 题型：选择题

已知向量与向量平行，则的值为（）

A． B． C． D．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

11．已知棱长为1的正方体ABCD-A₁B₁C₁D₁中，P，Q是面对角线A₁C₁的两个不同的动点．
①存在M，N两点，使BP⊥DQ；
②体对角线BD₁垂直平面DPQ；
③若|PQ|=1，S_△BPD∈[$\frac{\sqrt{2}}{2}$，$\frac{\sqrt{3}}{2}$]；
④若|PQ|=1，则四面体BDPQ在平面ABCD上的正投影面积为定值；
⑤若|PQ|=1，则四面体BDPQ的体积随着线段PQ移动而变化；
以上命题为真命题的有①②④．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

18．已知过点A（1，$\frac{3}{2}$）的椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点为F，且AF所在直线的斜率为$\frac{3}{4}$．
（1）求椭圆的C的方程；
（2）若存在直线l与椭圆交于两点M、N（均异于点A），使得∠MAN=90°，求证：直线l过定点．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

8．

我们通常把圆、椭圆、抛物线、双曲线统称为圆锥曲线．通过普通高中课程实验教科书《数学》2-1第二章《圆锥曲线与方程》章头引言我们知道，用一个垂直于圆锥的轴的平面截圆锥，截口曲线（截面与圆锥侧面的交线）是一个圆．实际上，设圆锥母线与轴所成角为α，不过圆锥顶点的截面与轴所成角为θ．当θ=$\frac{π}{2}$，截口曲线为圆，当$α＜θ＜\frac{π}{2}$时，截口曲线为椭圆；当0≤θ＜α时，截口曲线为双曲线；当θ=α时，截口曲线为抛物线；如图2，正方体ABCD-A′B′C′D′中，M为BC边的中点，点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′，那么点P的轨迹是（　　）

A．

一段双曲线弧

B．

一段椭圆弧

C．

一段圆弧

D．

一段抛物线弧

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

15．甲、乙等5名选手被随即分配到A、B、C、D四个不同的项目中，每个项目至少有一人，则甲乙两人同时参加A项目的概率为$\frac{1}{40}$．

查看答案和解析>>