
分析 P与A1点重合,Q与C1点重合,可判断①;体对角线BD1垂直平面A1C1D,可判断②;求出S△BPD的范围,可判断③;求出四面体BDPQ在平面ABCD上的正投影面积,可判断④;根据平面OBD将四面体BDPQ可分成两个底面均为平面OBD,高之和为PQ的棱锥(其中O为上底面中心),可判断⑤.
解答 解:当P与A1点重合,Q与C1点重合时,BP⊥DQ,
故①正确;
体对角线BD1垂直平面A1C1D,
即体对角线BD1垂直平面DPQ,
故②正确;
当P与A1重合时,S△BPD取最大值$\frac{\sqrt{3}}{2}$,
当Q与C1重合时,S△BPD取最小值$\frac{\sqrt{5-2\sqrt{2}}}{2}$,
即S△BPD∈[$\frac{\sqrt{5-2\sqrt{2}}}{2}$,$\frac{\sqrt{3}}{2}$];
故③错误;
④若|PQ|=1,则四面体BDPQ在平面ABCD上的正投影面积为定值$\frac{\sqrt{2}}{2}$;
故④正确;
设平面A1B1C1D1两条对角线交点为O,则易得PQ⊥平面OBD,
平面OBD将四面体BDPQ可分成两个底面均为平面OBD,
高之和为PQ的棱锥,故四面体BDPQ的体积一定是定值,
故⑤错误;
故答案为:①②④
点评 本题考查的知识点是棱柱的几何特征,是空间异面直线关系,棱锥体积,投影的综合应用,难度较大.


科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(理)试卷(解析版) 题型:解答题
执行如图所示的程序框图.
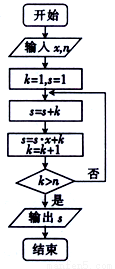
(1)若输入的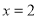 ,
,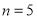 ,求输出的
,求输出的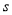 的值;
的值;
(2)若输入的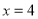 ,输出的
,输出的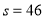 ,求输入的
,求输入的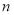 (
(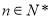 )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
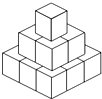 把14个棱长为1的正方体,在地面上堆叠成如图所示的几何体,然后将露出的表面部分染成红色.那么红色部分的面积为( )
把14个棱长为1的正方体,在地面上堆叠成如图所示的几何体,然后将露出的表面部分染成红色.那么红色部分的面积为( )| A. | .21 | B. | .24 | C. | .33 | D. | .37 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 直线三角形 | C. | 等腰三角形 | D. | 正三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com