
| A. | 锐角三角形 | B. | 直线三角形 | C. | 等腰三角形 | D. | 正三角形 |
分析 由 $\sqrt{3}$(acosB+bcosA)=2csinC及正弦定理可得 $\sqrt{3}$(sinAcosB+sinBcosA)=2sin2C,结合sinC>0,化简可得sinC=$\frac{\sqrt{3}}{2}$,由a+b=4,利用基本不等式可得ab≤4,(当且仅当a=b=2成立),由△ABC的面积的最大值S△ABC=$\frac{1}{2}$absinC≤$\frac{1}{2}$×4×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,即可解得a=b=2,从而得解△ABC的形状为等腰三角形.
解答 解:∵$\sqrt{3}$(acosB+bcosA)=2csinC,
∴$\sqrt{3}$(sinAcosB+sinBcosA)=2sin2C,
∴$\sqrt{3}$sinC=2sin2C,且sinC>0,
∴sinC=$\frac{\sqrt{3}}{2}$,
∵a+b=4,可得:4≥2 $\sqrt{ab}$,解得:ab≤4,(当且仅当a=b=2成立)
∵△ABC的面积的最大值S△ABC=$\frac{1}{2}$absinC≤$\frac{1}{2}$×4×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴a=b=2,
∴则此时△ABC的形状为等腰三角形.
故选:C.
点评 本题主要考查了正弦定理,三角形面积公式,基本不等式的应用,属于基本知识的考查.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 我们通常把圆、椭圆、抛物线、双曲线统称为圆锥曲线.通过普通高中课程实验教科书《数学》2-1第二章《圆锥曲线与方程》章头引言我们知道,用一个垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆.实际上,设圆锥母线与轴所成角为α,不过圆锥顶点的截面与轴所成角为θ.当θ=$\frac{π}{2}$,截口曲线为圆,当$α<θ<\frac{π}{2}$时,截口曲线为椭圆;当0≤θ<α时,截口曲线为双曲线; 当θ=α时,截口曲线为抛物线;如图2,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )
我们通常把圆、椭圆、抛物线、双曲线统称为圆锥曲线.通过普通高中课程实验教科书《数学》2-1第二章《圆锥曲线与方程》章头引言我们知道,用一个垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆.实际上,设圆锥母线与轴所成角为α,不过圆锥顶点的截面与轴所成角为θ.当θ=$\frac{π}{2}$,截口曲线为圆,当$α<θ<\frac{π}{2}$时,截口曲线为椭圆;当0≤θ<α时,截口曲线为双曲线; 当θ=α时,截口曲线为抛物线;如图2,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )| A. | 一段双曲线弧 | B. | 一段椭圆弧 | C. | 一段圆弧 | D. | 一段抛物线弧 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
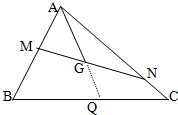 如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+y的最小值为( )
如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+y的最小值为( )| A. | 2 | B. | $\frac{1}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com