
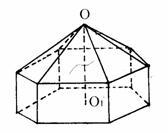
请您设计一个帐篷,它下部的形状是高为1m正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如下图所示)。试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积最大?
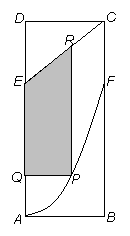
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
设命题p:方程x2+3x-1=0的两根符号不同;命题q:方程x2+3x-1=0的两根之和为3,判断命题“Øp”、“Øq”、“p∧q”、“p∨q”为假命题的个数为
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线l1: 4x-3y+6=0和直线l2: x=-1,抛物线y2=4x上一动点P,P到直线l1和直线l2的距离之和的最小值是
A.2 B.3 C.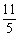 D.
D.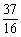
查看答案和解析>>
科目:高中数学 来源: 题型:
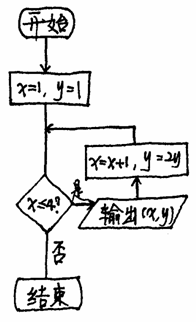
如图所示,程序框图输出的所有实数对(x, y)所对应的点都在函数
A.y=x+1的图象上 B.y=2x的图象上 C.y=2x的图象上 D.y=2x-1的图象上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com