
分析 (1)利用等比数列与等差数列的通项公式即可得出.
(2)由(1)得abn=a2n=$(\frac{1}{2})^{2n-2}$,利用abn<0.001,化简即可得出.
解答 解:(1)设{an}的公比为q,{bn}的公差为d,d>0.
∵b2=4a2,a2b3=6.∴2+d=4×2q,2q×(2+2d)=6,
解得d=2,q=$\frac{1}{2}$.
∴an=$2×(\frac{1}{2})^{n-1}$=$(\frac{1}{2})^{n-2}$,bn=2+2(n-1)=2n.
(2)由(1)得abn=a2n=$(\frac{1}{2})^{2n-2}$,
∵abn<0.001,
即$(\frac{1}{2})^{2n-2}$<0.001,∴22n-2>1 000,∴2n-2≥10,
即n≥6,∴满足题意的正整数n的最小值为6.
点评 本题考查了等差数列与等比数列的通项公式、不等式的解法,考查了推理能力与计算能力,属于中档题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:填空题
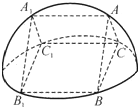 如图,直三棱柱ABC-A1B1C1的六个顶点都在半径为1的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为$\sqrt{2}$.
如图,直三棱柱ABC-A1B1C1的六个顶点都在半径为1的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要但不充分条件 | B. | 充分但不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2] | B. | (1,+∞) | C. | (2,+∞) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,2x>x2 | B. | 若a>b,c>d,则 a-c>b-d | ||
| C. | ?x∈R,ex<0 | D. | ac2<bc2是a<b的充分不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com